Difference between revisions of "1987 AIME Problems/Problem 4"
(→Solution) |
Hastapasta (talk | contribs) |
||
| Line 2: | Line 2: | ||
Find the [[area]] of the region enclosed by the [[graph]] of <math>|x-60|+|y|=\left|\frac{x}{4}\right|.</math> | Find the [[area]] of the region enclosed by the [[graph]] of <math>|x-60|+|y|=\left|\frac{x}{4}\right|.</math> | ||
| − | == Solution == | + | == Solution 1 == |
[[Image:1987_AIME-4.png]] | [[Image:1987_AIME-4.png]] | ||
| Line 11: | Line 11: | ||
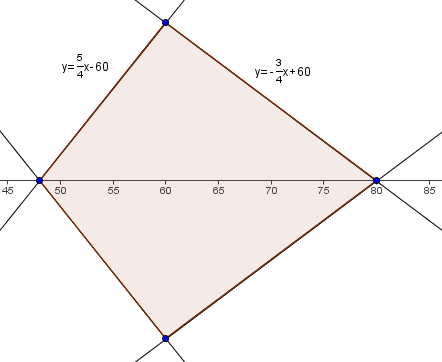
The area of the region enclosed by the graph is that of the quadrilateral defined by the points <math>(48,0),\ (60,15),\ (80,0), \ (60,-15)</math>. Breaking it up into triangles and solving or using shoelace, we get <math>2 \cdot \frac{1}{2}(80 - 48)(15) = \boxed{480}</math>. | The area of the region enclosed by the graph is that of the quadrilateral defined by the points <math>(48,0),\ (60,15),\ (80,0), \ (60,-15)</math>. Breaking it up into triangles and solving or using shoelace, we get <math>2 \cdot \frac{1}{2}(80 - 48)(15) = \boxed{480}</math>. | ||
| + | |||
| + | == Solution 2 == | ||
| + | |||
| + | Since <math>|y|</math> is the only present <math>y</math> "term" in this equation, we know that the area must be symmetrical about the x-axis. | ||
| + | |||
| + | We'll consider the area when <math>y>0</math> and we only consider the portion enclosed with <math>y=0</math>. Then, we'll double that area since the graph is symmetrical. | ||
| + | |||
| + | Now, let us remove the absolute values: | ||
| + | |||
| + | When <math>x>60</math> or <math>x=60</math>: <math>x-60+y=0.25x</math>. This rearranges to <math>y=-0.75x+60</math>. | ||
| + | |||
| + | When <math>0<=x<60</math>: <math>60-x+y=0.25</math>. So <math>y=1.25x-60</math>. | ||
| + | |||
| + | When <math>x<0</math>: <math>60-x+y=-0.25x</math>. So <math>y=0.75x-60</math>. | ||
| + | |||
| + | By simple sketching, we see the shape that looks like the image in Solution 1 (graph it out and you'll see). We see that the partial area we seek in this part is the triangle with the vertices <math>(60,15)</math>, <math>(48,0)</math>, <math>(80,0)</math>. This triangle has an area of <math>(80-48)*15*0.5=240</math>. | ||
| + | |||
| + | Simply double the area and we get 480 as our final answer. I can't box the answer for some reason. Please let me know what's wrong. | ||
| + | |||
| + | ~hastapasta | ||
== See also == | == See also == | ||
Revision as of 13:18, 2 February 2022
Contents
Problem
Find the area of the region enclosed by the graph of ![]()
Solution 1
Since ![]() is nonnegative,
is nonnegative, ![]() . Solving this gives us two equations:
. Solving this gives us two equations: ![]() . Thus,
. Thus, ![]() . The maximum and minimum y value is when
. The maximum and minimum y value is when ![]() , which is when
, which is when ![]() and
and ![]() . Since the graph is symmetric about the y-axis, we just need casework upon
. Since the graph is symmetric about the y-axis, we just need casework upon ![]() .
. ![]() , so we break up the condition
, so we break up the condition ![]() :
:
 . Then
. Then  .
. . Then
. Then  .
.
The area of the region enclosed by the graph is that of the quadrilateral defined by the points ![]() . Breaking it up into triangles and solving or using shoelace, we get
. Breaking it up into triangles and solving or using shoelace, we get ![]() .
.
Solution 2
Since ![]() is the only present
is the only present ![]() "term" in this equation, we know that the area must be symmetrical about the x-axis.
"term" in this equation, we know that the area must be symmetrical about the x-axis.
We'll consider the area when ![]() and we only consider the portion enclosed with
and we only consider the portion enclosed with ![]() . Then, we'll double that area since the graph is symmetrical.
. Then, we'll double that area since the graph is symmetrical.
Now, let us remove the absolute values:
When ![]() or
or ![]() :
: ![]() . This rearranges to
. This rearranges to ![]() .
.
When ![]() :
: ![]() . So
. So ![]() .
.
When ![]() :
: ![]() . So
. So ![]() .
.
By simple sketching, we see the shape that looks like the image in Solution 1 (graph it out and you'll see). We see that the partial area we seek in this part is the triangle with the vertices ![]() ,
, ![]() ,
, ![]() . This triangle has an area of
. This triangle has an area of ![]() .
.
Simply double the area and we get 480 as our final answer. I can't box the answer for some reason. Please let me know what's wrong.
~hastapasta
See also
| 1987 AIME (Problems • Answer Key • Resources) | ||
| Preceded by Problem 3 |
Followed by Problem 5 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.