Asymptote: Useful commands and their Output

Asymptote (Vector Graphics Language)

Getting Started - Basics - Drawing - Labeling - Filling - Useful functions - Examples - Macros and Packages Help - Reference - Advanced Asymptote - 3D Graphics - CSE5 Package - How to

For more complicated examples, which are often quite neat, see this page in the Art of Problem Solving Test Forum, which has various diagrams from contests. Clicking on them will reveal the code used to make them, so this is an excellent resource for students looking to make more advanced diagrams.

For each of the following, we have put a blue dot at the origin in order to indicate relative location of the output on the coordinate plane. In other words, assume that before each of the examples below is the command

dot((0,0),blue);

In addition, a comment after a line such as //math - extension indicates that the command (in this case extension) used in that line is defined in the math package, thus motivating the import math; (or other appropriate package) line at the top of the example.

---

Example 1:

dot((20,0));

Output 1:

---

Example 2:

draw((0,0)--(50,0),BeginArrow);
draw((0,-10)--(50,-10),MidArrow);
draw((0,-20)--(50,-20),EndArrow);
draw((0,-30)--(50,-30),Arrows);

Output 2:

---

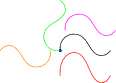
Example 3:

draw((0,0)--(50,0));
arrow((30,0),dir(180),green);

Output 3:

---

Example 4:

import math;
pair A,B,C,D,E;
A=(0,0); C=(50,0); B=(10,10); D=(40,20);
E=extension(A,B,C,D);  // math - extension
// extension(A,B,C,D) returns the intersection of lines AB and CD
draw(A--B); draw(C--D);
draw(B--E--D,orange);

Output 4:

---

Example 5:

import graph;
draw(Circle((0,0),20)); // graph - Circle

Output 5:

---

Example 6:

path p=(0,0)..(20,15)..(40,-5)..(50,0);
draw(p);
draw(rotate(90)*p,green);
draw(rotate(180,(-5,0))*p,orange);
draw(shift((5,20))*p,magenta);
draw(shift((0,-25))*yscale(1.4)*p,red);

Output 6:

---

Example 7:

import olympiad;
unitsize(50);
pair A,B,C,O,I;
A=origin; B=2*right; C=1.5*dir(70);
O=circumcenter(A,B,C); // olympiad - circumcenter
I=incenter(A,B,C); // olympiad - incenter
draw(A--B--C--cycle);
dot(O);
dot(I);
draw(circumcircle(A,B,C)); // olympiad - circumcircle
draw(incircle(A,B,C)); // olympiad - incircle
label("$I$",I,W);
label("$O$",O,S);

Output 7:

---

Example 8:

import three;
unitsize(1cm);
size(50);
currentprojection=orthographic(1/2,-1,1/2); // three - currentprojection, orthographic
draw((0,0,0)--(1,0,0)--(1,1,0)--(0,1,0)--cycle,red);
draw((0,0,0)--(0,0,1));
draw((0,1,0)--(0,1,1));
draw((1,1,0)--(1,1,1));
draw((1,0,0)--(1,0,1));
draw((0,0,1)--(1,0,1)--(1,1,1)--(0,1,1)--cycle,green);

Output 8:

---

Example 10, buildcycle: fill(buildcycle(curveI,reverse(curveIII),curveII),yellow);

Output 10, buildcycle:

Examples in Forum

Clicking on the images the the forum or on images here in the previous examples will show you as to-copy-and-paste the Asymptote source. (For this you have to be registered at artofproblemsolving.com.)

Triangles, lines, tick marks, angle marks

See Also

Many more Asymptote examples

Next: Macros and Packages