Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2003 AMC 12B Problems/Problem 21"

(→‎Solution 2)
m (→‎Solution 2)
Line 23: Line 23:
 
<math>WLOG</math>, let the object turn clockwise.
 
<math>WLOG</math>, let the object turn clockwise.
  
−
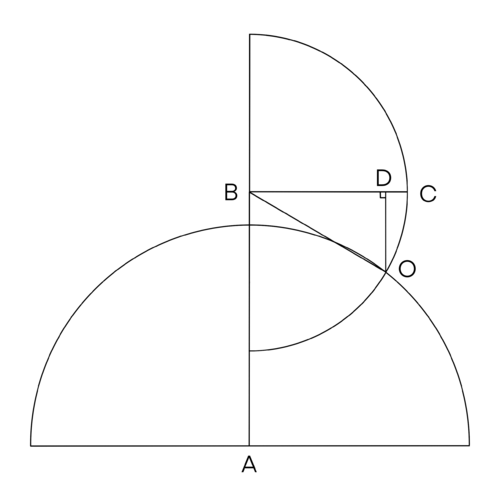
Note that the possible points of <math>C</math> create a semi-circle of radius <math>5</math> and center <math>B</math>. The area where <math>AC < 7</math> is enclosed by a circle of radius <math>7</math> center <math>A</math>.
+
Note that the possible points of <math>C</math> create a semi-circle of radius <math>5</math> and center <math>B</math>. The area where <math>AC < 7</math> is enclosed by a circle of radius <math>7</math> and center <math>A</math>. The probability that <math>AC < 7</math> is <math></math>\frac{\angle ABO}{180 ^\circ}<math>.
  
−
Let <math>B = (0, 0)</math>. Function of <math>\odot B = x^2 + y^2 = 25</math>, function of <math>\odot A = x^2 + (y+8)^2 = 49</math>.
+
Let </math>B = (0, 0)<math>. The function of </math>\odot B = x^2 + y^2 = 25<math>, the function of </math>\odot A = x^2 + (y+8)^2 = 49<math>.
  
−
<math>O</math> is the point that satisfies both functions.
+
</math>O<math> is the point that satisfies both functions.
  
−
<math>x^2 + (y+8)^2 - x^2 - y^2 = 49 - 25</math>, <math>64 + 16y =24</math>, <math>y = - \frac52</math>, <math>x = \frac{5 \sqrt{3}}{2}</math>, <math>O = (\frac{5 \sqrt{3}}{2}, - \frac52)</math>
+
</math>x^2 + (y+8)^2 - x^2 - y^2 = 49 - 25<math>, </math>64 + 16y =24<math>, </math>y = - \frac52<math>, </math>x = \frac{5 \sqrt{3}}{2}<math>, </math>O = (\frac{5 \sqrt{3}}{2}, - \frac52)<math>
  
−
Note that <math>\triangle BDO</math> is a <math>30-60-90</math> triangle, as <math>BO = 5</math>, <math>BD = \frac{5 \sqrt{3}}{2}</math>, <math>DO = \frac52</math>. As a result <math>\angle CBO = 30 ^\circ</math>, <math>\angle ABO = 60 ^\circ</math>.
+
Note that </math>\triangle BDO<math> is a </math>30-60-90<math> triangle, as </math>BO = 5<math>, </math>BD = \frac{5 \sqrt{3}}{2}<math>, </math>DO = \frac52<math>. As a result </math>\angle CBO = 30 ^\circ<math>, </math>\angle ABO = 60 ^\circ<math>.
  
−
Therefore the probability that <math>AC < 7</math> is <math>\frac{\angle ABO}{180 ^\circ} = \frac{60 ^\circ}{180 ^\circ} = \boxed{\textbf{(D) } \frac13 }</math>
+
Therefore the probability that </math>AC < 7<math> is </math>\frac{\angle ABO}{180 ^\circ} = \frac{60 ^\circ}{180 ^\circ} = \boxed{\textbf{(D) } \frac13 }$
  
 
~[https://artofproblemsolving.com/wiki/index.php/User:Isabelchen isabelchen]
 
~[https://artofproblemsolving.com/wiki/index.php/User:Isabelchen isabelchen]

Revision as of 10:53, 31 August 2022

Problem

An object moves $8$ cm in a straight line from $A$ to $B$, turns at an angle $\alpha$, measured in radians and chosen at random from the interval $(0,\pi)$, and moves $5$ cm in a straight line to $C$. What is the probability that $AC < 7$?

$\mathrm{(A)}\ \frac{1}{6} \qquad\mathrm{(B)}\ \frac{1}{5} \qquad\mathrm{(C)}\ \frac{1}{4} \qquad\mathrm{(D)}\ \frac{1}{3} \qquad\mathrm{(E)}\ \frac{1}{2}$

Solution 1 (Trigonometry)

By the Law of Cosines, \begin{align*} AB^2 + BC^2 - 2 AB \cdot BC \cos \alpha = 89 - 80 \cos \alpha = AC^2 &< 49\\ \cos \alpha &> \frac 12\\ \end{align*}

It follows that $0 < \alpha < \frac {\pi}3$, and the probability is $\frac{\pi/3}{\pi} = \frac 13 \Rightarrow \mathrm{(D)}$.

Solution 2

2003AMC12BP21.png

$WLOG$, let the object turn clockwise.

Note that the possible points of $C$ create a semi-circle of radius $5$ and center $B$. The area where $AC < 7$ is enclosed by a circle of radius $7$ and center $A$. The probability that $AC < 7$ is $$ (Error compiling LaTeX. Unknown error_msg)\frac{\angle ABO}{180 ^\circ}$.

Let$ (Error compiling LaTeX. Unknown error_msg)B = (0, 0)$. The function of$\odot B = x^2 + y^2 = 25$, the function of$\odot A = x^2 + (y+8)^2 = 49$.$O$is the point that satisfies both functions.$x^2 + (y+8)^2 - x^2 - y^2 = 49 - 25$,$64 + 16y =24$,$y = - \frac52$,$x = \frac{5 \sqrt{3}}{2}$,$O = (\frac{5 \sqrt{3}}{2}, - \frac52)$Note that$\triangle BDO$is a$30-60-90$triangle, as$BO = 5$,$BD = \frac{5 \sqrt{3}}{2}$,$DO = \frac52$. As a result$\angle CBO = 30 ^\circ$,$\angle ABO = 60 ^\circ$.

Therefore the probability that$ (Error compiling LaTeX. Unknown error_msg)AC < 7$is$\frac{\angle ABO}{180 ^\circ} = \frac{60 ^\circ}{180 ^\circ} = \boxed{\textbf{(D) } \frac13 }$

~isabelchen

See also

2003 AMC 12B (Problems • Answer Key • Resources)
Preceded by
Problem 20 		Followed by
Problem 22
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2003_AMC_12B_Problems/Problem_21&oldid=177778"