Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2006 Cyprus MO/Lyceum/Problem 19"

(New page: ==Problem== {{empty}} ==Solution== {{solution}} ==See also== {{CYMO box|year=2006|l=Lyceum|num-b=18|num-a=20}})
 
(solution)
Line 1: Line 1:
 
==Problem==
 
==Problem==
−
{{empty}}
+
<div style="float:right">
 +
[[Image:2006 CyMO-19.PNG|250px]]
 +
</div>
 +
 
 +
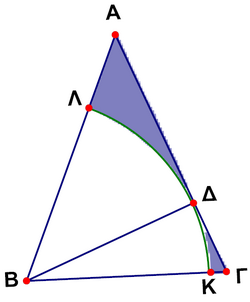
In the figure <math>ABC</math> is isosceles triangle with<math> AB=AC=\sqrt2</math> and <math>\ang A=45^\circ</math>. If <math>BD</math> is altitude of the triangle and the sector <math>BLDKB</math> belongs to the circle <math>(B,BD)</math>, the area of the shaded region is
 +
 
 +
A. <math>\frac{4\sqrt3-\pi}{6}</math>
 +
 
 +
B. <math>4\left(\sqrt2-\frac{\pi}{3}\right)</math>
 +
 
 +
C. <math>\frac{8\sqrt2-3\pi}{16}</math>
 +
 
 +
D. <math>\frac{\pi}{8}</math>
 +
 
 +
E. None of these
  
 
==Solution==
 
==Solution==
−
{{solution}}
+
<math>ADB</math> is a [[right triangle]] with an angle of <math>45^{\circ}</math>, so it is a <math>45-45-90 \triangle</math> and <math>BD = \frac{AB}{\sqrt{2}} = 1</math>. The area of the entire circle is <math>(1)^2\pi = \pi</math>. To find the area of the sector, we find the central angle is <math>\frac{180-45}{2} = \frac{135}{2}</math>, and the area is <math>\frac{\frac{135}{2}}{360} = \frac{3}{16}\pi</math>. The area of the entire triangle is <math>\frac{1}{2}bh = \frac{\sqrt{2}}{2}</math>. Thus the answer is <math>\frac{\sqrt{2}}{2} - \frac{3}{16}\pi = \frac{8\sqrt{2} - 3\pi}{16} \Longrightarrow \mathrm{(C)}</math>.
−
 
+
 
==See also==
 
==See also==
 
{{CYMO box|year=2006|l=Lyceum|num-b=18|num-a=20}}
 
{{CYMO box|year=2006|l=Lyceum|num-b=18|num-a=20}}
 +
 +
[[Category:Introductory Geometry Problems]]

Revision as of 18:07, 15 October 2007

Problem

2006 CyMO-19.PNG

In the figure $ABC$ is isosceles triangle with$AB=AC=\sqrt2$ and $\ang A=45^\circ$ (Error compiling LaTeX. Unknown error_msg). If $BD$ is altitude of the triangle and the sector $BLDKB$ belongs to the circle $(B,BD)$, the area of the shaded region is

A. $\frac{4\sqrt3-\pi}{6}$

B. $4\left(\sqrt2-\frac{\pi}{3}\right)$

C. $\frac{8\sqrt2-3\pi}{16}$

D. $\frac{\pi}{8}$

E. None of these

Solution

$ADB$ is a right triangle with an angle of $45^{\circ}$, so it is a $45-45-90 \triangle$ and $BD = \frac{AB}{\sqrt{2}} = 1$. The area of the entire circle is $(1)^2\pi = \pi$. To find the area of the sector, we find the central angle is $\frac{180-45}{2} = \frac{135}{2}$, and the area is $\frac{\frac{135}{2}}{360} = \frac{3}{16}\pi$. The area of the entire triangle is $\frac{1}{2}bh = \frac{\sqrt{2}}{2}$. Thus the answer is $\frac{\sqrt{2}}{2} - \frac{3}{16}\pi = \frac{8\sqrt{2} - 3\pi}{16} \Longrightarrow \mathrm{(C)}$.

See also

2006 Cyprus MO, Lyceum (Problems)
Preceded by
Problem 18 		Followed by
Problem 20
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 • 26 • 27 • 28 • 29 • 30
Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2006_Cyprus_MO/Lyceum/Problem_19&oldid=18160"