Difference between revisions of "2006 Cyprus MO/Lyceum/Problem 19"
(→Problem) |
(→Problem) |
||
| Line 4: | Line 4: | ||
</div> | </div> | ||
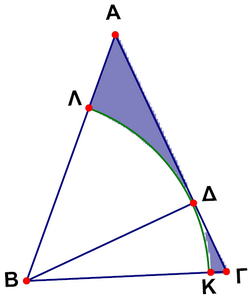
| − | In the figure <math>AB\ | + | In the figure <math>AB\Lambda</math> is isosceles triangle with<math> AB=A\Lambda=\sqrt2</math> and <math>\ang A=45^\circ</math>. If <math>BD</math> is altitude of the triangle and the sector <math>BLDKB</math> belongs to the circle <math>(B,BD)</math>, the area of the shaded region is |
A. <math>\frac{4\sqrt3-\pi}{6}</math> | A. <math>\frac{4\sqrt3-\pi}{6}</math> | ||
Revision as of 07:17, 16 October 2007
Problem
In the figure 
is isosceles triangle with
and $\ang A=45^\circ$ (Error compiling LaTeX. Unknown error_msg). If 
is altitude of the triangle and the sector 
belongs to the circle 
, the area of the shaded region is
A. 
B. 
C. 
D. 
E. None of these
Solution
is a right triangle with an angle of 
, so it is a 
and 
. The area of the entire circle is 
. To find the area of the sector, we find the central angle is 
, and the area is 
. The area of the entire triangle is 
. Thus the answer is 
.
See also
| 2006 Cyprus MO, Lyceum (Problems) | ||
| Preceded by Problem 18 |
Followed by Problem 20 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 • 26 • 27 • 28 • 29 • 30 | ||
