Difference between revisions of "2023 AMC 8 Problems/Problem 17"
(→Video Solution by OmegaLearn (Using 3D Visualization)) |
Grapecoder (talk | contribs) (Tag: Undo) |
||
| Line 1: | Line 1: | ||
==Problem== | ==Problem== | ||
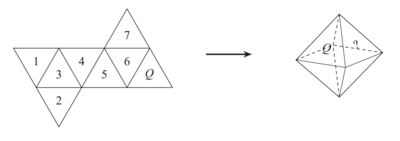
| − | A regular octahedron has eight equilateral triangle faces with four faces meeting at each vertex. Jun will make the regular octahedrons shown on the right by folding the piece of paper shown on the left. Which numbered face will end up to the right of Q? | + | A ''regular octahedron'' has eight equilateral triangle faces with four faces meeting at each vertex. Jun will make the regular octahedrons shown on the right by folding the piece of paper shown on the left. Which numbered face will end up to the right of <math>Q</math>? |
| − | < | + | [[Image:2023 AMC 8-17.png|thumb|center|400px]] |
| + | |||
| + | ==Solution (Intuition)== | ||
| + | The answer is <math>\boxed{\textbf{(A)}\ 1}.</math> Use intuition to bring it down to <math>2</math> guesses <math>1</math> or <math>2</math> and guess from there or you could actually fold the paper. | ||
==Animated Video Solution== | ==Animated Video Solution== | ||
| Line 9: | Line 12: | ||
~Star League (https://starleague.us) | ~Star League (https://starleague.us) | ||
| − | + | ==Video Solution by OmegaLearn (Using 3D Visualization)== | |
| + | https://youtu.be/gIjhiw1CUgY | ||
==See Also== | ==See Also== | ||
{{AMC8 box|year=2023|num-b=16|num-a=18}} | {{AMC8 box|year=2023|num-b=16|num-a=18}} | ||
{{MAA Notice}} | {{MAA Notice}} | ||
Revision as of 05:08, 25 January 2023
Contents
[hide]Problem
A regular octahedron has eight equilateral triangle faces with four faces meeting at each vertex. Jun will make the regular octahedrons shown on the right by folding the piece of paper shown on the left. Which numbered face will end up to the right of ![]() ?
?
Solution (Intuition)
The answer is ![]() Use intuition to bring it down to
Use intuition to bring it down to ![]() guesses
guesses ![]() or
or ![]() and guess from there or you could actually fold the paper.
and guess from there or you could actually fold the paper.
Animated Video Solution
~Star League (https://starleague.us)
Video Solution by OmegaLearn (Using 3D Visualization)
See Also
| 2023 AMC 8 (Problems • Answer Key • Resources) | ||
| Preceded by Problem 16 |
Followed by Problem 18 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AJHSME/AMC 8 Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()