Difference between revisions of "2023 AMC 8 Problems/Problem 9"
Irorlpiggy (talk | contribs) |
(→Solution) |
||
| Line 4: | Line 4: | ||
<math>\textbf{(A)}\ 6 \qquad \textbf{(B)}\ 8 \qquad \textbf{(C)}\ 10 \qquad \textbf{(D)}\ 12 \qquad \textbf{(E)}\ 14</math> | <math>\textbf{(A)}\ 6 \qquad \textbf{(B)}\ 8 \qquad \textbf{(C)}\ 10 \qquad \textbf{(D)}\ 12 \qquad \textbf{(E)}\ 14</math> | ||
| − | ==Solution== | + | ==Solution 1== |
The time intervals in which Malaika's elevation is between <math>4</math> and <math>7</math> meters are: | The time intervals in which Malaika's elevation is between <math>4</math> and <math>7</math> meters are: | ||
| Line 16: | Line 16: | ||
~apex304, MRENTHUSIASM | ~apex304, MRENTHUSIASM | ||
| + | |||
| + | ==Solution 2== | ||
| + | |||
| + | We count the number of seconds and get <math>\boxed{\textbf{(B)}\ 8}</math> | ||
| + | |||
| + | Solution by [[User:ILoveMath31415926535|ILoveMath31415926535]] | ||
== Video Solution 1 by SpreadTheMathLove== | == Video Solution 1 by SpreadTheMathLove== | ||
Revision as of 11:16, 25 January 2023
Contents
[hide]Problem
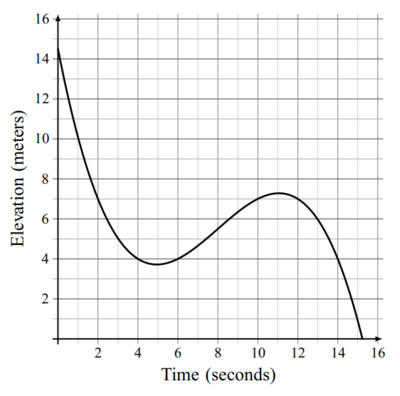
Malaika is skiing on a mountain. The graph below shows her elevation, in meters, above the base of the mountain as she skis along a trail. In total, how many seconds does she spend at an elevation between ![]() and
and ![]() meters?
meters?
![]()
Solution 1
The time intervals in which Malaika's elevation is between ![]() and
and ![]() meters are:
meters are:
- from the
 nd to the
nd to the  th seconds
th seconds
- from the
 th to the
th to the  th seconds
th seconds
- from the
 th to the
th to the  th seconds
th seconds
In total, Malaika spends ![]() seconds at such elevation.
seconds at such elevation.
~apex304, MRENTHUSIASM
Solution 2
We count the number of seconds and get ![]()
Solution by ILoveMath31415926535
Video Solution 1 by SpreadTheMathLove
https://www.youtube.com/watch?v=lfyg5ZMV0gg
Video Solution by Magic Square
https://youtu.be/-N46BeEKaCQ?t=4903
See Also
| 2023 AMC 8 (Problems • Answer Key • Resources) | ||
| Preceded by Problem 8 |
Followed by Problem 10 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AJHSME/AMC 8 Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()