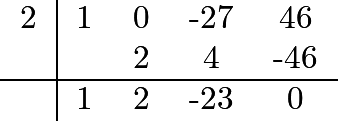Difference between revisions of "2024 AIME I Problems/Problem 15"
(problem) |
m (Grammar) |
||
| Line 1: | Line 1: | ||
==Problem== | ==Problem== | ||
| − | Let <math>\textit{B}</math> be the set of rectangular boxes with surface area <math>54</math> and volume <math>23</math>. Let <math>r</math> be the smallest sphere that can contain each of the rectangular boxes that are elements of <math>\textit{B}</math>. The value of <math>r^2</math> can be written as <math>\frac{p}{q}</math>, where <math>p</math> and <math>q</math> are relatively prime positive integers. Find <math>p+q</math>. | + | Let <math>\textit{B}</math> be the set of rectangular boxes with surface area <math>54</math> and volume <math>23</math>. Let <math>r</math> be the radius of the smallest sphere that can contain each of the rectangular boxes that are elements of <math>\textit{B}</math>. The value of <math>r^2</math> can be written as <math>\frac{p}{q}</math>, where <math>p</math> and <math>q</math> are relatively prime positive integers. Find <math>p+q</math>. |
==Solution 1== | ==Solution 1== | ||
Revision as of 19:30, 2 February 2024
Problem
Let ![]() be the set of rectangular boxes with surface area
be the set of rectangular boxes with surface area ![]() and volume
and volume ![]() . Let
. Let ![]() be the radius of the smallest sphere that can contain each of the rectangular boxes that are elements of
be the radius of the smallest sphere that can contain each of the rectangular boxes that are elements of ![]() . The value of
. The value of ![]() can be written as
can be written as ![]() , where
, where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]() .
.
Solution 1
Observe that the "worst" possible box is one of the maximum possible length.
By symmetry, the height and the width are the same in this antioptimal box. (If the height and width weren't the same, the extra difference between them could be used to make the length longer.) Thus, let the width and height be of length ![]() and the length be
and the length be ![]() .
.
We're given that the volume is ![]() ; thus,
; thus, ![]() . We're also given that the surface area is
. We're also given that the surface area is ![]() ; thus,
; thus, ![]() .
.
From the first equation, we can get ![]() . We do a bunch of algebra:
. We do a bunch of algebra:
We can use the Rational Root Theorem and test a few values. It turns out that ![]() works. We use synthetic division to divide by
works. We use synthetic division to divide by ![]() :
:
As we expect, the remainder is ![]() , and we are left with the polynomial
, and we are left with the polynomial ![]() . We can now simply use the quadratic formula and find that the remaining roots are
. We can now simply use the quadratic formula and find that the remaining roots are ![]() . We want the smallest
. We want the smallest ![]() to maximize
to maximize ![]() , and it turns out that
, and it turns out that ![]() is in fact the smallest root. Thus, we let
is in fact the smallest root. Thus, we let ![]() . Substituting this into
. Substituting this into ![]() , we find that
, we find that ![]() . However, this is not our answer! This is simply the length of the box; we want the radius of the sphere enclosing it. We know that the diameter of the sphere is the diagonal of the box, and the 3D Pythagorean Theorem can give us the space diagonal. Applying it, we find that the diagonal has length
. However, this is not our answer! This is simply the length of the box; we want the radius of the sphere enclosing it. We know that the diameter of the sphere is the diagonal of the box, and the 3D Pythagorean Theorem can give us the space diagonal. Applying it, we find that the diagonal has length  . This is the diameter; we halve it to find the radius,
. This is the diameter; we halve it to find the radius, ![]() . We then square this and end up with
. We then square this and end up with ![]() , giving us an answer of
, giving us an answer of ![]() .
.
~Technodoggo
See also
| 2024 AIME I (Problems • Answer Key • Resources) | ||
| Preceded by Problem 14 |
Followed by Last Problem | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()