Difference between revisions of "Trigonometry"
(→Basic definitions: Added csc, sec, and cot. Changed "base" to "opposite side" and "altitude" to "adjacent side" since the angle theta is not always the topmost angle.) |
(→Basic definitions: added image of a 30-60-90 triangle) |
||
| Line 8: | Line 8: | ||
i.e. If ABC is a right triangle with right angle C, and angle A = <math>\displaystyle \theta</math>, then BC is the "opposite side", AC is the "adjacent side", and AB is the hypotenuse. | i.e. If ABC is a right triangle with right angle C, and angle A = <math>\displaystyle \theta</math>, then BC is the "opposite side", AC is the "adjacent side", and AB is the hypotenuse. | ||
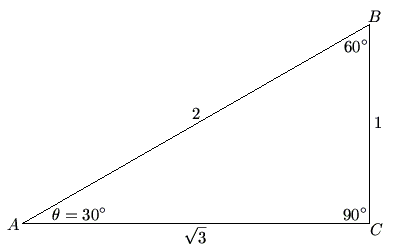
| − | + | [[Image:306090triangle.gif]] | |
===[[Sine]]=== | ===[[Sine]]=== | ||
Revision as of 21:40, 23 June 2006
Trigonometry seeks to find the lengths of a triangle's sides, given 2 angles and a side. Trigonometry is closely related to analytic geometry.
Contents
[hide]Basic definitions
Usually we call an angle ![]() , read "theta", but
, read "theta", but ![]() is just a variable. We could just as well call it
is just a variable. We could just as well call it ![]() .
.
For the following definitions, the "opposite side" is the side opposite of angle ![]() and the "adjacent side" is the side that is part of angle
and the "adjacent side" is the side that is part of angle ![]() but is not the hypotenuse.
but is not the hypotenuse.
i.e. If ABC is a right triangle with right angle C, and angle A = ![]() , then BC is the "opposite side", AC is the "adjacent side", and AB is the hypotenuse.
, then BC is the "opposite side", AC is the "adjacent side", and AB is the hypotenuse.
Sine
The sine of an angle ![]() , abbreviated
, abbreviated ![]() , is the ratio between the opposite side and the hypotenuse of a triangle. For instance, in the 30-60-90 triangle above,
, is the ratio between the opposite side and the hypotenuse of a triangle. For instance, in the 30-60-90 triangle above, ![]() .
.
Cosine
The cosine of an angle ![]() , abbreviated
, abbreviated ![]() , is the ratio between the adjacent side and the hypotenuse of a triangle. For instance, in the 30-60-90 triangle above,
, is the ratio between the adjacent side and the hypotenuse of a triangle. For instance, in the 30-60-90 triangle above, ![]() .
.
Tangent
The tangent of an angle ![]() , abbreviated
, abbreviated ![]() , is the ratio between the opposite side and the adjacent side of a triangle. For instance, in the 30-60-90 triangle above,
, is the ratio between the opposite side and the adjacent side of a triangle. For instance, in the 30-60-90 triangle above, ![]() . (Note that
. (Note that ![]() .)
.)
Cosecant
The cosecant of an angle ![]() , abbreviated
, abbreviated ![]() , is the ratio between the hypotenuse and the opposite side of a triangle. For instance, in the 30-60-90 triangle above,
, is the ratio between the hypotenuse and the opposite side of a triangle. For instance, in the 30-60-90 triangle above, ![]() . (Note that
. (Note that ![]() .)
.)
Secant
The secant of an angle ![]() , abbreviated
, abbreviated ![]() , is the ratio between the hypotenuse and the adjacent side of a triangle. For instance, in the 30-60-90 triangle above,
, is the ratio between the hypotenuse and the adjacent side of a triangle. For instance, in the 30-60-90 triangle above, ![]() . (Note that
. (Note that ![]() .)
.)
Cotangent
The cotangent of an angle ![]() , abbreviated
, abbreviated ![]() , is the ratio between the adjacent side and the opposite side of a triangle. For instance, in the 30-60-90 triangle above,
, is the ratio between the adjacent side and the opposite side of a triangle. For instance, in the 30-60-90 triangle above, ![]() . (Note that
. (Note that ![]() .)
.)