Difference between revisions of "1998 AIME Problems/Problem 6"
(→Solution) |
|||
| Line 1: | Line 1: | ||
== Problem == | == Problem == | ||
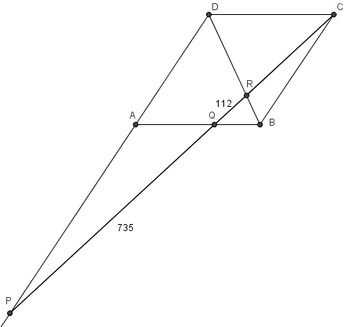
| − | Let <math> | + | Let <math>ABCD</math> be a [[parallelogram]]. Extend <math>\overline{DA}</math> through <math>A</math> to a point <math>P,</math> and let <math>\overline{PC}</math> meet <math>\overline{AB}</math> at <math>Q</math> and <math>\overline{DB}</math> at <math>R.</math> Given that <math>PQ = 735</math> and <math>QR = 112,</math> find <math>RC.</math> |
== Solution == | == Solution == | ||
| Line 39: | Line 39: | ||
[[Category:Intermediate Geometry Problems]] | [[Category:Intermediate Geometry Problems]] | ||
| + | {{MAA Notice}} | ||
Latest revision as of 18:38, 4 July 2013
Contents
[hide]Problem
Let ![]() be a parallelogram. Extend
be a parallelogram. Extend ![]() through
through ![]() to a point
to a point ![]() and let
and let ![]() meet
meet ![]() at
at ![]() and
and ![]() at
at ![]() Given that
Given that ![]() and
and ![]() find
find ![]()
Solution
Solution 1
There are several similar triangles. ![]() , so we can write the proportion:
, so we can write the proportion:
![]()
Also, ![]() , so:
, so:
![]()
![]()
Substituting,
![]()
![]()
![]()
Thus, ![]() .
.
Solution 2
We have ![]() so
so ![]() . We also have
. We also have ![]() so
so ![]() . Equating the two results gives
. Equating the two results gives ![]() and so
and so ![]() which solves to
which solves to ![]()
See also
| 1998 AIME (Problems • Answer Key • Resources) | ||
| Preceded by Problem 5 |
Followed by Problem 7 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.