Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2007 AIME II Problems/Problem 3"

m (fmt a bit)
Line 1: Line 1:
 
== Problem ==
 
== Problem ==
−
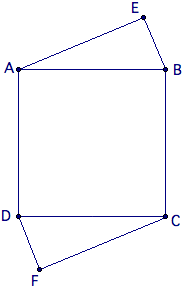
[[Square]] <math>ABCD</math> has side length <math>13</math>, and [[point]]s <math>E</math> and <math>F</math> are exterior to the square such that <math>BE=DF=5</math> and <math>AE=CF=12</math>. Find <math>\displaystyle EF^{2}</math>.
+
[[Square]] <math>ABCD</math> has side length <math>13</math>, and [[point]]s <math>E</math> and <math>F</math> are exterior to the square such that <math>BE=DF=5</math> and <math>AE=CF=12</math>. Find <math>EF^{2}</math>.
  
 
<div style="text-align:center;">[[Image:2007 AIME II-3.png]]</div>
 
<div style="text-align:center;">[[Image:2007 AIME II-3.png]]</div>
Line 29: Line 29:
  
 
[[Category:Intermediate Geometry Problems]]
 
[[Category:Intermediate Geometry Problems]]
 +
{{MAA Notice}}

Revision as of 22:32, 4 July 2013

Problem

Square $ABCD$ has side length $13$, and points $E$ and $F$ are exterior to the square such that $BE=DF=5$ and $AE=CF=12$. Find $EF^{2}$.

2007 AIME II-3.png

Solution

Solution 1

Extend $\overline{AE}, \overline{DF}$ and $\overline{BE}, \overline{CF}$ to their points of intersection. Since $\triangle ABE \cong \triangle CDF$ and are both $5-12-13$ right triangles, we can come to the conclusion that the two new triangles are also congruent to these two (use ASA, as we know all the sides are $13$ and the angles are mostly complementary). Thus, we create a square with sides $5 + 12 = 17$.

2007 AIME II-3b.PNG

$\overline{EF}$ is the diagonal of the square, with length $17\sqrt{2}$; the answer is $EF^2 = (17\sqrt{2})^2 = 578$.


Solution 2

A slightly more analytic/brute-force approach:

AIME II prob10 bruteforce.PNG

Drop perpendiculars from $E$ and $F$ to $I$ and $J$, respectively; construct right triangle $EKF$ with right angle at K and $EK || BC$. Since $2[CDF]=DF*CF=CD*JF$, we have $JF=5\times12/13 = \frac{60}{13}$. Similarly, $EI=\frac{60}{13}$. Since $\triangle DJF \sim \triangle DFC$, we have $DJ=\frac{5JF}{12}=\frac{25}{13}$.

Now, we see that $FK=DC-(DJ+IB)=DC-2DJ=13-\frac{50}{13}=\frac{119}{13}$. Also, $EK=BC+(JF+IE)=BC+2JF=13+\frac{120}{13}=\frac{289}{13}$. By the Pythagorean Theorem, we have $EF=\sqrt{\left(\frac{289}{13}\right)^2+\left(\frac{119}{13} \right)^2}=\frac{\sqrt{(17^2)(17^2+7^2)}}{13}$$=\frac{17\sqrt{338}}{13}=\frac{17(13\sqrt{2})}{13}=17\sqrt{2}$. Therefore, $EF^2=(17\sqrt{2})^2=578$.

See also

2007 AIME II (Problems • Answer Key • Resources)
Preceded by
Problem 2 		Followed by
Problem 4
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2007_AIME_II_Problems/Problem_3&oldid=55436"