1990 AIME Problems/Problem 14
Problem
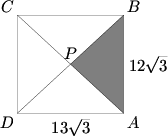
The rectangle ![]() below has dimensions
below has dimensions ![]() and
and ![]() . Diagonals
. Diagonals ![]() and
and ![]() intersect at
intersect at ![]() . If triangle
. If triangle ![]() is cut out and removed, edges
is cut out and removed, edges ![]() and
and ![]() are joined, and the figure is then creased along segments
are joined, and the figure is then creased along segments ![]() and
and ![]() , we obtain a triangular pyramid, all four of whose faces are isosceles triangles. Find the volume of this pyramid.
, we obtain a triangular pyramid, all four of whose faces are isosceles triangles. Find the volume of this pyramid.
Solution
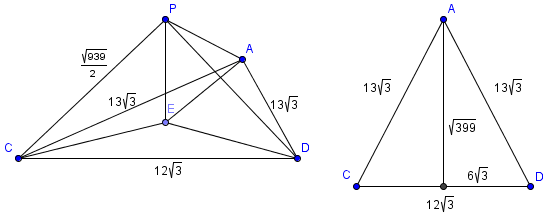
Our triangular pyramid has base ![]() . The area of this isosceles triangle is easy to find by
. The area of this isosceles triangle is easy to find by ![]() , where we can find
, where we can find ![]() to be
to be ![]() by the Pythagorean Theorem. Thus
by the Pythagorean Theorem. Thus ![]() .
.
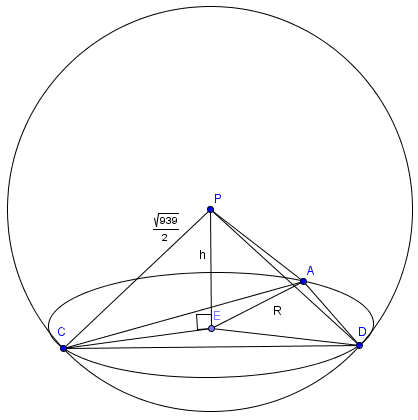
To find the volume, we want to use the equation ![]() , so we need to find the height of the tetrahedron. By the Pythagorean Theorem,
, so we need to find the height of the tetrahedron. By the Pythagorean Theorem, ![]() . If we let
. If we let ![]() be the center of a sphere with radius
be the center of a sphere with radius ![]() , then
, then ![]() lie on the sphere. The cross section of the sphere is a circle, and the center of that circle is the foot of the perpendicular from the center of the sphere. Hence the foot of the height we want to find occurs at the circumcenter of
lie on the sphere. The cross section of the sphere is a circle, and the center of that circle is the foot of the perpendicular from the center of the sphere. Hence the foot of the height we want to find occurs at the circumcenter of ![]() .
.
From here we just need to perform some brutish calculations. Using the formula ![]() (
(![]() being the circumradius), we find
being the circumradius), we find ![]() . By the Pythagorean Theorem,
. By the Pythagorean Theorem,

Finally, we substitute ![]() into the volume equation to find
into the volume equation to find ![]() .
.
See also
| 1990 AIME (Problems • Answer Key • Resources) | ||
| Preceded by Problem 13 |
Followed by Problem 15 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||