2007 AIME II Problems/Problem 3
Problem
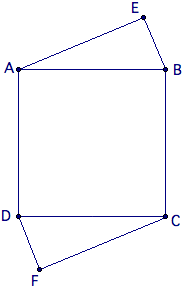
Square ![]() has side length
has side length ![]() , and points
, and points ![]() and
and ![]() are exterior to the square such that
are exterior to the square such that ![]() and
and ![]() . Find
. Find ![]() .
.
Solution
Extend ![]() and
and ![]() to their points of intersection. Since
to their points of intersection. Since ![]() and are both
and are both ![]() right triangles, we can come to the conclusion that the two new triangles are also congruent to these two (use ASA, as we know all the sides are
right triangles, we can come to the conclusion that the two new triangles are also congruent to these two (use ASA, as we know all the sides are ![]() and the angles are mostly complementary). Thus, we create a square with sides
and the angles are mostly complementary). Thus, we create a square with sides ![]() .
.
![]() is the diagonal of the square, with length
is the diagonal of the square, with length ![]() ; the answer is
; the answer is ![]() .
.
See also
| 2007 AIME II (Problems • Answer Key • Resources) | ||
| Preceded by Problem 2 |
Followed by Problem 4 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||