Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

2011 AMC 10B Problems/Problem 22

Revision as of 17:37, 19 September 2021 by Williamwu001 (talk | contribs) (→‎Solution 2)

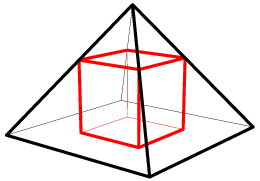
Problem

A pyramid has a square base with sides of length $1$ and has lateral faces that are equilateral triangles. A cube is placed within the pyramid so that one face is on the base of the pyramid and its opposite face has all its edges on the lateral faces of the pyramid. What is the volume of this cube?

$\textbf{(A)}\ 5\sqrt{2} - 7 \qquad\textbf{(B)}\ 7 - 4\sqrt{3} \qquad\textbf{(C)}\ \frac{2\sqrt{2}}{27} \qquad\textbf{(D)}\ \frac{\sqrt{2}}{9} \qquad\textbf{(E)}\ \frac{\sqrt{3}}{9}$

Solution 1

It is often easier to first draw a diagram for such a problem.

2011AMC10B22.png

Sometimes, it may also be easier to think of the problem in 2D. Take a cross section of the pyramid through the apex and two points from the base that are opposite to each other. Place it in two dimensions.

[asy] unitsize(35mm); defaultpen(linewidth(2pt)+fontsize(10pt)); pair A=(0,0), B=(sqrt(2),0), C=(0.5sqrt(2),0.5sqrt(2)); pair W=(sqrt(2)-1,0), X=(1,0), Y=(1,sqrt(2)-1), Z=(sqrt(2)-1,sqrt(2)-1); draw(A--B--C--cycle); draw(W--X--Y--Z--cycle,red); [/asy]

The dimensions of this triangle are $1, 1,$ and $\sqrt{2}$ because the sidelengths of the pyramid are $1$ and the base of the triangle is the diagonal of the pyramid's base. This is a $45-45-90$ triangle. Also, we can let the dimensions of the rectangle be $s$ and $s\sqrt{2}$ because the longer length was the diagonal of the cube's base and the shorter length was a side of the cube.

[asy] unitsize(35mm); defaultpen(linewidth(2pt)+fontsize(12pt)); pair A=(0,0), B=(sqrt(2),0), C=(0.5sqrt(2),0.5sqrt(2)); pair W=(sqrt(2)-1,0), X=(1,0), Y=(1,sqrt(2)-1), Z=(sqrt(2)-1,sqrt(2)-1); draw(A--B--C--cycle); draw(W--X--Y--Z--cycle,red); label("$1$",(A--C),NW); label("$1$",(B--C),NE); label("$\sqrt{2}$",(A--B),S); label("$s$",(W--Z),E,red); label("$s$",(X--Y),W,red); label("$s\sqrt{2}$",(W--X),N,red); [/asy]

The two triangles on the right and left of the rectangle are also $45-45-90$ triangles because the rectangle is perpendicular to the base, and they share a $45^\circ$ angle with the larger triangle. Therefore, the legs of the right triangles can be expressed as $s.$

[asy] unitsize(35mm); defaultpen(linewidth(2pt)+fontsize(12pt)); pair A=(0,0), B=(sqrt(2),0), C=(0.5sqrt(2),0.5sqrt(2)); pair W=(sqrt(2)-1,0), X=(1,0), Y=(1,sqrt(2)-1), Z=(sqrt(2)-1,sqrt(2)-1); draw(A--B--C--cycle); draw(W--X--Y--Z--cycle,red); label("$1$",(A--C),NW); label("$1$",(B--C),NE); label("$\sqrt{2}$",(A--B),S); label("$s$",(W--Z),E,red); label("$s$",(X--Y),W,red); label("$s\sqrt{2}$",(W--X),N,red); label("$s$",(A--W),N); label("$s$",(X--B),N); [/asy]

Now we can just use segment addition to find the value of $s.$ \[\sqrt{2}=s+s\sqrt{2}+s=2s+s\sqrt{2}=(2+\sqrt{2})s\] \[s=\frac{\sqrt{2}}{2+\sqrt{2}}=\frac{1}{\sqrt{2}+1}=\frac{\sqrt{2}-1}{2-1}=\sqrt{2}-1\]

The volume of the cube is $s^3 = (\sqrt{2}-1)^3 = (\sqrt{2}-1)(3-2\sqrt{2}) = 3\sqrt{2}-3-4+2\sqrt{2} = \boxed{\textbf{(A)} 5\sqrt{2}-7}$

Solution 2

Let $s$ be the slant height and $d$ be the distance from one side of the base to the point right under the apex. Then using the Pythagorean Theorem, the altitude from the apex to the base is \[a=\sqrt{s^2-d^2}=\sqrt{\left(\dfrac{\sqrt{3}}{2}\right)^2-\left(\dfrac{1}{2}\right)^2}=\dfrac{\sqrt{2}}{2}\] Notice that the smaller pyramid on top of the cube is similar to the larger pyramid. Thus, letting $x$ be the edge length of the cube, then the altitude of the smaller pyramid is $\dfrac{\sqrt{2}}{2}\cdot{\dfrac{x}{1}}=\dfrac{\sqrt{2}}{2}$.

Since the altitude of the larger pyramid is the sum of the edge length of the cube and the altitude of the smaller pyramid, we have \[\dfrac{\sqrt{2}}{2}=x+\dfrac{\sqrt{2}}{2}x\] \[x=\sqrt{2}-1\]

Finally, $V_{cube}=x^3=(\sqrt{2}-1)^3=\boxed{\textbf{(A)} 5\sqrt{2}-7}$

~ Nafer (Minor edits by anonymous)

See Also

2011 AMC 10B (Problems • Answer Key • Resources)
Preceded by
Problem 21 		Followed by
Problem 23
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 10 Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2011_AMC_10B_Problems/Problem_22&oldid=162468"