2006 Cyprus MO/Lyceum/Problem 7

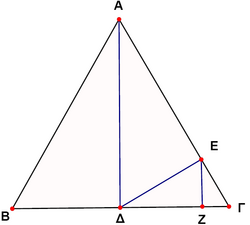
Problem

In the figure, $AB\Gamma$ is an equilateral triangle and $A\Delta \perp B\Gamma$ , $\Delta E\perp A\Gamma$ , $EZ\perp B\Gamma$ . If $EZ=\sqrt{3}$ , then the length of the side of the triangle $AB\Gamma$ is

$\mathrm{(A)}\ \frac{3\sqrt{3}}{2}\qquad\mathrm{(B)}\ 8\qquad\mathrm{(C)}\ 4\qquad\mathrm{(D)}\ 3\qquad\mathrm{(E)}\ 9$

Solution

$\triangle EZ\Gamma$ is a $30-60-90$ right triangle, so $Z\Gamma = \frac{\sqrt{3}}{\sqrt{3}} = 1$ . Also $\angle ZE\Delta = 90 - 30 = 60^{\circ}$ , so $\triangle ZE\Delta$ also is a $30-60-90 \triangle$ .

Thus, $\Delta Z = \sqrt{3} \cdot \sqrt{3} = 3$ . Adding, $\Delta Z + Z\Gamma = 4$ , and a side of $\triangle AB\Gamma$ is $2 \Delta \Gamma = 8\ \mathrm{(B)}$ .

2006 Cyprus MO, Lyceum (Problems)
Preceded by Problem 6	Followed by Problem 8
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 • 26 • 27 • 28 • 29 • 30

Page

Toolbox

Search

2006 Cyprus MO/Lyceum/Problem 7

Problem

Solution

See also