1987 AIME Problems
Contents
Problem 1
An ordered pair ![]() of non-negative integers is called "simple" if the addition
of non-negative integers is called "simple" if the addition ![]() in base
in base ![]() requires no carrying. Find the number of simple ordered pairs of non-negative integers that sum to
requires no carrying. Find the number of simple ordered pairs of non-negative integers that sum to ![]() .
.
Problem 2
What is the largest possible distance between two points, one on the sphere of radius 19 with center ![]() and the other on the sphere of radius 87 with center
and the other on the sphere of radius 87 with center ![]() ?
?
Problem 3
By a proper divisior of a natural number we mean a positive integral divisor other than 1 and the number itself. A natural number greater than 1 will be called "nice" if it is equal to the product of its distinct proper divisors. What is the sum of the first ten nice numbers?
Problem 4
Find the area of the region enclosed by the graph of ![]()
Problem 5
Find ![]() if
if ![]() and
and ![]() are integers such that
are integers such that ![]() .
.
Problem 6
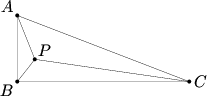
Rectangle ![]() is divided into four parts of equal area by five segments as shown in the figure, where
is divided into four parts of equal area by five segments as shown in the figure, where ![]() , and
, and ![]() is parallel to
is parallel to ![]() . Find the length of
. Find the length of ![]() (in cm) if
(in cm) if ![]() cm and
cm and ![]() cm.
cm.
Problem 7
Let ![]() denote the least common multiple of positive integers
denote the least common multiple of positive integers ![]() and
and ![]() . Find the number of ordered triples
. Find the number of ordered triples ![]() of positive integers for which
of positive integers for which ![]() ,
, ![]() , and
, and ![]() .
.
Problem 8
What is the largest positive integer ![]() for which there is a unique integer
for which there is a unique integer ![]() such that
such that ![]() ?
?
Problem 9
Triangle ![]() has right angle at
has right angle at ![]() , and contains a point
, and contains a point ![]() for which
for which ![]() ,
, ![]() , and
, and ![]() . Find
. Find ![]() .
.
Problem 10
Al walks down to the bottom of an escalator that is moving up and he counts 150 steps. His friend, Bob, walks up to the top of the escalator and counts 75 steps. If Al's speed of walking (in steps per unit time) is three times Bob's walking speed, how many steps are visible on the escalator at a given time? (Assume that this value is constant.)
Problem 11
Find the largest possible value of ![]() for which
for which ![]() is expressible as the sum of
is expressible as the sum of ![]() consecutive positive integers.
consecutive positive integers.
Problem 12
Let ![]() be the smallest integer whose cube root is of the form
be the smallest integer whose cube root is of the form ![]() , where
, where ![]() is a positive integer and
is a positive integer and ![]() is a positive real number less than
is a positive real number less than ![]() . Find
. Find ![]() .
.
Problem 13
A given sequence ![]() of distinct real numbers can be put in ascending order by means of one or more "bubble passes". A bubble pass through a given sequence consists of comparing the second term with the first term, and exchanging them if and only if the second term is smaller, then comparing the third term with the second term and exchanging them if and only if the third term is smaller, and so on in order, through comparing the last term,
of distinct real numbers can be put in ascending order by means of one or more "bubble passes". A bubble pass through a given sequence consists of comparing the second term with the first term, and exchanging them if and only if the second term is smaller, then comparing the third term with the second term and exchanging them if and only if the third term is smaller, and so on in order, through comparing the last term, ![]() , with its current predecessor and exchanging them if and only if the last term is smaller.
, with its current predecessor and exchanging them if and only if the last term is smaller.
The example below shows how the sequence 1, 9, 8, 7 is transformed into the sequence 1, 8, 7, 9 by one bubble pass. The numbers compared at each step are underlined.
Suppose that ![]() , and that the terms of the initial sequence
, and that the terms of the initial sequence ![]() are distinct from one another and are in random order. Let
are distinct from one another and are in random order. Let ![]() , in lowest terms, be the probability that the number that begins as
, in lowest terms, be the probability that the number that begins as ![]() will end up, after one bubble pass, in the
will end up, after one bubble pass, in the ![]() place. Find
place. Find ![]() .
.
Problem 14
Compute
.
Problem 15
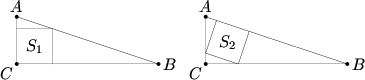
Squares ![]() and
and ![]() are inscribed in right triangle
are inscribed in right triangle ![]() , as shown in the figures below. Find
, as shown in the figures below. Find ![]() if area
if area ![]() and area
and area ![]() .
.