2006 Cyprus MO/Lyceum/Problem 19
Problem
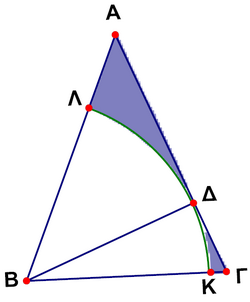
In the figure ![]() is isosceles triangle with
is isosceles triangle with![]() and $\ang A=45^\circ$ (Error compiling LaTeX. Unknown error_msg). If
and $\ang A=45^\circ$ (Error compiling LaTeX. Unknown error_msg). If ![]() is altitude of the triangle and the sector
is altitude of the triangle and the sector ![]() belongs to the circle
belongs to the circle ![]() , the area of the shaded region is
, the area of the shaded region is
A. ![]()
B. ![]()
C. ![]()
D. ![]()
E. None of these
Solution
![]() is a right triangle with an angle of
is a right triangle with an angle of ![]() , so it is a
, so it is a ![]() and
and ![]() . The area of the entire circle is
. The area of the entire circle is ![]() . To find the area of the sector, we find the central angle is
. To find the area of the sector, we find the central angle is ![]() , and the area is
, and the area is ![]() . The area of the entire triangle is
. The area of the entire triangle is ![]() . Thus the answer is
. Thus the answer is ![]() .
.
See also
| 2006 Cyprus MO, Lyceum (Problems) | ||
| Preceded by Problem 18 |
Followed by Problem 20 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 • 26 • 27 • 28 • 29 • 30 | ||