2007 AIME I Problems/Problem 15
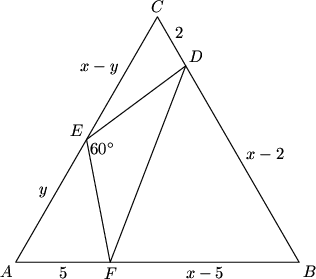
Problem
Let ![]() be an equilateral triangle, and let
be an equilateral triangle, and let ![]() and
and ![]() be points on sides
be points on sides ![]() and
and ![]() , respectively, with
, respectively, with ![]() and
and ![]() . Point
. Point ![]() lies on side
lies on side ![]() such that angle
such that angle ![]() . The area of triangle
. The area of triangle ![]() is
is ![]() . The two possible values of the length of side
. The two possible values of the length of side ![]() are
are ![]() , where
, where ![]() and
and ![]() are rational, and
are rational, and ![]() is an integer not divisible by the square of a prime. Find
is an integer not divisible by the square of a prime. Find ![]() .
.
Solution
Denote the length of a side of the triangle ![]() , and of
, and of ![]() as
as ![]() . The area of the entire equilateral triangle is
. The area of the entire equilateral triangle is ![]() . Add up the areas of the triangles using the
. Add up the areas of the triangles using the ![]() formula (notice that for the three outside triangles,
formula (notice that for the three outside triangles, ![]() ):
): ![]() . This simplifies to
. This simplifies to ![]() . Some terms will cancel out, leaving
. Some terms will cancel out, leaving ![]() .
.
![]() is an external angle to
is an external angle to ![]() , from which we find that
, from which we find that ![]() , so
, so ![]() . Similarly, we find that
. Similarly, we find that ![]() . Thus,
. Thus, ![]() . Setting up a ratio of sides, we get that
. Setting up a ratio of sides, we get that ![]() . Using the previous relationship between
. Using the previous relationship between ![]() and
and ![]() , we can solve for
, we can solve for ![]() .
.
![]()
![]()
![]()
![]()
Use the quadratic formula, though we only need the root of the discriminant. This is ![]()
![]() . The answer is
. The answer is ![]() .
.
See also
| 2007 AIME I (Problems • Answer Key • Resources) | ||
| Preceded by Problem 14 |
Followed by Last Question | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()