Jadhav Angular Formula

Jadhav Angular Formula evaluates the angle between any two sides of any triangle given length of all the sides, invented by Indian mathematical scholar Jyotiraditya Jadhav.

Introduction

In any triangle given sides a,b and c , with longest side c the angle between the sides a and b can be found by:

$\measuredangle = \cos^-1 [{a^2+b^2-c^2}(2ab)^-1]$

Nomenclature:

Cosine function : The cosine function is one of the basic functions encountered in trigonometry (the others being the cosecant , cotangent, secant, sine , and tangent ). Let be an angle measured counterclockwise from the x -axis along the arc of the unit circle . Then is the horizontal coordinate of the arc endpoint.
$a^2$ : square of length of one side among the angle
$b^2$ : square of length of other side among the angle

$c^2$ : square of length of the longest side/ opposite side to the angle

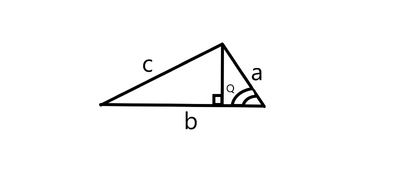
Visual use

Jadhav Angular Formula

Let the angle angle between side length a and b be Q

Now as per the equation angle Q will be:

$\measuredangle Q = \arccos [a^2+b^2-c^2/2ab]$

Applications

Astrophysics: For finding angles between the vector of celestial bodies.

Aerodynamics: In finding the glide angle, angle of climb and various angles of attack.

Navigation: In finding real time locations.

Geography: In calculating distances between geographical locations.
Geometry: In finding angles between the two sides of any triangle.

Robotics: In operating arms and for studying robotic movements through vectors.
Teleportation and Quantum Physics: In studying oscillating motions of particles.

Other inventions by Jyotiraditya Jadhav

Read more about Jyotiraditya Jadhav here.

Page

Toolbox

Search

Jadhav Angular Formula

Contents

Introduction

Nomenclature:

Visual use

Applications

Other inventions by Jyotiraditya Jadhav