Asymptote: Useful commands and their Output
For more complicated examples, which are often quite neat, see this page in the Art of Problem Solving Test Forum, which has various diagrams from contests. Clicking on them will reveal the code used to make them, so this is an excellent resource for students looking to make more advanced diagrams. Also check out the AoPS Asymptote Quick Start Video.
For each of the following, we have put a blue dot at the origin in order to indicate relative location of the output on the coordinate plane. In other words, assume that before each of the examples below is the command
dot((0,0),blue);
In addition, a comment after a line such as //math - extension indicates that the command (in this case extension) used in that line is defined in the math package, thus motivating the import math; (or other appropriate package) line at the top of the example.
Example 1:
unitsize(1.5 cm);
real ticklength = 3;
pair D, S;
D = (3,3); S = (0,0);
draw((-1,0)--(4,0),EndArrow(5)); draw((0,-1)--(0,4),EndArrow(5));
label("Interest rate", (4,0), E); label("Money supply", (0,4), N);
draw((0,0)--D--(3.5,3.5),dashed); draw((3.5,0)--(3.5,3.5),dashed);
label("Easy monetary policy", (1.75,1.75), NE, red); label("Tight monetary policy", (3.75,0.25), E, red);
Output 1:
![[asy] size(2cm); unitsize(1.5 cm); real ticklength = 3; pair D, S; D = (3,3); S = (0,0); draw((-1,0)--(4,0),EndArrow(5)); draw((0,-1)--(0,4),EndArrow(5)); label("Interest rate", (4,0), E); label("Money supply", (0,4), N); draw((0,0)--D--(3.5,3.5),dashed); draw((3.5,0)--(3.5,3.5),dashed); label("Easy monetary policy", (1.75,1.75), NE, red); label("Tight monetary policy", (3.75,0.25), E, red); [/asy]](http://latex.artofproblemsolving.com/9/b/5/9b50b08ac4994e66bdec36fe4bfff4008ac74b9a.png)
Example 2:
unitsize(1.5 cm);
real ticklength = 3;
pair D, S;
D = (3,3); S = (0,0);
draw((-1,0)--(4,0),EndArrow(5)); draw((0,-1)--(0,4),EndArrow(5));
label("Government expenditure", (4,0), E); label("Aggregate demand", (0,4), N);
draw((0,0)--D--(3.5,3.5),dashed); draw((3.5,0)--(3.5,3.5),dashed);
label("Expansionary fiscal policy", (1.75,1.75), NE, red); label("Contractionary fiscal policy", (3.75,0.25), E, red);
Output 2:
![[asy]unitsize(1.5 cm); real ticklength = 3; pair D, S; D = (3,3); S = (0,0); draw((-1,0)--(4,0),EndArrow(5)); draw((0,-1)--(0,4),EndArrow(5)); label("Government expenditure", (4,0), E); label("Aggregate demand", (0,4), N); draw((0,0)--D--(3.5,3.5),dashed); draw((3.5,0)--(3.5,3.5),dashed); label("Expansionary fiscal policy", (1.75,1.75), NE, red); label("Contractionary fiscal policy", (3.75,0.25), E, red); [/asy]](http://latex.artofproblemsolving.com/b/e/4/be4079a51ad7fc34f48cbaf070a23a106af28596.png)
Example 3:
draw((0,0)--(50,0)); arrow((30,0),dir(180),green);
Example 4:
import math; pair A,B,C,D,E; A=(0,0); C=(50,0); B=(10,10); D=(40,20); E=extension(A,B,C,D); // math - extension // extension(A,B,C,D) returns the intersection of lines AB and CD draw(A--B); draw(C--D); draw(B--E--D,orange);
Example 5:
import graph; draw(Circle((0,0),20)); // graph - Circle
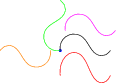
Example 6:
path p=(0,0)..(20,15)..(40,-5)..(50,0); draw(p); draw(rotate(90)*p,green); draw(rotate(180,(-5,0))*p,orange); draw(shift((5,20))*p,magenta); draw(shift((0,-25))*yscale(1.4)*p,red);
Example 7:
import olympiad;
unitsize(50);
pair A,B,C,O,I;
A=origin; B=2*right; C=1.5*dir(70);
O=circumcenter(A,B,C); // olympiad - circumcenter
I=incenter(A,B,C); // olympiad - incenter
draw(A--B--C--cycle);
dot(O);
dot(I);
draw(circumcircle(A,B,C)); // olympiad - circumcircle
draw(incircle(A,B,C)); // olympiad - incircle
label("$I$",I,W);
label("$O$",O,S);
Output 7:
![[asy] import olympiad; size(75); pair A,B,C,O,I; A=origin; B=2*right; C=1.5*dir(70); O=circumcenter(A,B,C); /* olympiad - circumcenter */ I=incenter(A,B,C); /* olympiad - incenter */ draw(A--B--C--cycle); dot(O); dot(I); draw(circumcircle(A,B,C)); /* olympiad - circumcircle */ draw(incircle(A,B,C)); /* olympiad - incircle */ label("$I$",I,W); label("$O$",O,S); [/asy]](http://latex.artofproblemsolving.com/5/2/6/526c2646a25ae53a5308fc46f81a53976f51030c.png)
Example 8:
import three; unitsize(1cm); size(50); currentprojection=orthographic(1/2,-1,1/2); // three - currentprojection, orthographic draw((0,0,0)--(1,0,0)--(1,1,0)--(0,1,0)--cycle,red); draw((0,0,0)--(0,0,1)); draw((0,1,0)--(0,1,1)); draw((1,1,0)--(1,1,1)); draw((1,0,0)--(1,0,1)); draw((0,0,1)--(1,0,1)--(1,1,1)--(0,1,1)--cycle,green);
Output 8:
![[asy] import three; unitsize(1cm); size(50); currentprojection=orthographic(1/2,-1,1/2); // three - currentprojection, orthographic draw((0,0,0)--(1,0,0)--(1,1,0)--(0,1,0)--cycle,red); draw((0,0,0)--(0,0,1)); draw((0,1,0)--(0,1,1)); draw((1,1,0)--(1,1,1)); draw((1,0,0)--(1,0,1)); draw((0,0,1)--(1,0,1)--(1,1,1)--(0,1,1)--cycle,green); [/asy]](http://latex.artofproblemsolving.com/1/1/f/11fb26b90e43cef283c6a3dcdb09dd8684ad893f.png)
Example 10, buildcycle:
fill(buildcycle(curveI,reverse(curveIII),curveII),yellow);
Output 10, buildcycle:
![[asy] unitsize(1cm); pair A1=(2,5),A2=(10,1); pair B1=(1,1),B2=(10,5); pair C1=(1,2),C2=(10,3.5); path curveI = A1 .. controls (6,5) .. A2; path curveII = B1 .. controls (3,4) .. B2; path curveIII = C1 .. controls (3,3) and (7,0) .. (9,2) ..controls C2 .. C2; fill(buildcycle(curveI,reverse(curveIII),curveII),yellow); draw(curveI, red); draw(curveII, blue); draw(curveIII, green); pair ip_1 = intersectionpoint(curveI, curveII); pair ip_2 = intersectionpoint(curveII, curveIII); pair ip_3 = intersectionpoint(curveI, curveIII); label("$A_1$",A1,1.5W,red); label("$A_2$",A2,1SE,red); label("$B_1$",B1,1.5SSW,heavyblue); label("$B_2$",B2,1.12E,heavyblue); label("$C_1$",C1,1.5W,heavygreen); label("$C_2$",C2,1.25E,heavygreen); dot(ip_1^^ip_2^^ip_3); label("$S_1$",ip_1, 1.5*NNE); label("$S_2$",ip_2, 1.5*SSE); label("$S_3$",ip_3, 1.85*dir(-93)); dot(A1^^A2, mediumred); dot(B1^^B2, mediumblue); dot(C1^^C2, mediumgreen); [/asy]](http://latex.artofproblemsolving.com/3/4/d/34d5b1e9735496d0efea02709ee44543e7b49439.png)
Examples in Forum
Clicking on Asymptote images the forums will show you the Asymptote source code, which can be copy-pasted.
Triangles, lines, tick marks, angle marks
See Also
Many more Asymptote examples (Links to an external site)