2019 AIME I Problems/Problem 15
Contents
[hide]Problem
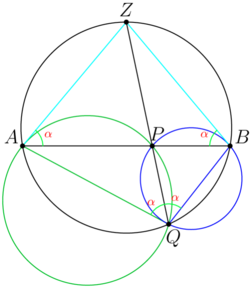
Let ![]() be a chord of a circle
be a chord of a circle ![]() , and let
, and let ![]() be a point on the chord
be a point on the chord ![]() . Circle
. Circle ![]() passes through
passes through ![]() and
and ![]() and is internally tangent to
and is internally tangent to ![]() . Circle
. Circle ![]() passes through
passes through ![]() and
and ![]() and is internally tangent to
and is internally tangent to ![]() . Circles
. Circles ![]() and
and ![]() intersect at points
intersect at points ![]() and
and ![]() . Line
. Line ![]() intersects
intersects ![]() at
at ![]() and
and ![]() . Assume that
. Assume that ![]() ,
, ![]() ,
, ![]() , and
, and ![]() , where
, where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]() .
.
Solution 1
![[asy] size(8cm); pair O, A, B, P, O1, O2, Q, X, Y; O=(0, 0); A=dir(140); B=dir(40); P=(3A+5B)/8; O1=extension((A+P)/2, (A+P)/2+(0, 1), A, O); O2=extension((B+P)/2, (B+P)/2+(0, 1), B, O); Q=intersectionpoints(circle(O1, length(A-O1)), circle(O2, length(B-O2)))[1]; X=intersectionpoint(P -- (P+(P-Q)*100), circle(O, 1)); Y=intersectionpoint(Q -- (Q+(Q-P)*100), circle(O, 1)); draw(circle(O, 1)); draw(circle(O1, length(A-O1))); draw(circle(O2, length(B-O2))); draw(A -- B); draw(X -- Y); draw(A -- O -- B); draw(O1 -- P -- O2); dot("$O$", O, S); dot("$A$", A, A); dot("$B$", B, B); dot("$P$", P, dir(70)); dot("$Q$", Q, dir(200)); dot("$O_1$", O1, SW); dot("$O_2$", O2, SE); dot("$X$", X, X); dot("$Y$", Y, Y); [/asy]](http://latex.artofproblemsolving.com/e/9/6/e962da47468c53887e591467b64d5b0b0fe4dde6.png) Let
Let ![]() and
and ![]() be the centers of
be the centers of ![]() and
and ![]() , respectively. There is a homothety at
, respectively. There is a homothety at ![]() sending
sending ![]() to
to ![]() that sends
that sends ![]() to
to ![]() and
and ![]() to
to ![]() , so
, so ![]() . Similarly,
. Similarly, ![]() , so
, so ![]() is a parallelogram. Moreover,
is a parallelogram. Moreover, ![]() whence
whence ![]() is cyclic. However,
is cyclic. However, ![]() so
so ![]() is an isosceles trapezoid. Since
is an isosceles trapezoid. Since ![]() ,
, ![]() , so
, so ![]() is the midpoint of
is the midpoint of ![]() .
.
By Power of a Point, ![]() . Since
. Since ![]() and
and ![]() ,
, ![]() and the requested sum is
and the requested sum is ![]() .
.
(Solution by TheUltimate123)
Note
One may solve for ![]() first using PoAP,
first using PoAP, ![]() . Then, notice that
. Then, notice that ![]() is rational but
is rational but ![]() is not, also
is not, also ![]() . The most likely explanation for this is that
. The most likely explanation for this is that ![]() is the midpoint of
is the midpoint of ![]() , so that
, so that ![]() and
and ![]() . Then our answer is
. Then our answer is ![]() . One can rigorously prove this using the methods above
. One can rigorously prove this using the methods above
Solution 2
Let the tangents to ![]() at
at ![]() and
and ![]() intersect at
intersect at ![]() . Then, since
. Then, since ![]() ,
, ![]() lies on the radical axis of
lies on the radical axis of ![]() and
and ![]() , which is
, which is ![]() . It follows that
. It follows that ![]() Let
Let ![]() denote the midpoint of
denote the midpoint of ![]() . By the Midpoint of Harmonic Bundles Lemma(EGMO 9.17),
. By the Midpoint of Harmonic Bundles Lemma(EGMO 9.17), ![]() whence
whence ![]() . Like above,
. Like above, ![]() . Since
. Since ![]() , we establish that
, we establish that ![]() , from which
, from which ![]() , and the requested sum is
, and the requested sum is ![]() .
.
(Solution by TheUltimate123)
Solution 3
Firstly we need to notice that ![]() is the middle point of
is the middle point of ![]() . Assume the center of circle
. Assume the center of circle ![]() are
are ![]() , respectively. Then
, respectively. Then ![]() are collinear and
are collinear and ![]() are collinear. Link
are collinear. Link ![]() . Notice that,
. Notice that, ![]() . As a result,
. As a result, ![]() and
and ![]() . So we have parallelogram
. So we have parallelogram ![]() . So
. So ![]() Notice that,
Notice that, ![]() and
and ![]() divides
divides ![]() into two equal length pieces, So we have
into two equal length pieces, So we have ![]() . As a result,
. As a result, ![]() lie on one circle. So
lie on one circle. So ![]() . Notice that since
. Notice that since ![]() , we have
, we have ![]() . As a result,
. As a result, ![]() . So
. So ![]() is the middle point of
is the middle point of ![]() .
.
Back to our problem. Assume ![]() ,
, ![]() and
and ![]() . Then we have
. Then we have ![]() , that is,
, that is, ![]() . Also,
. Also, ![]() . Solve these above, we have
. Solve these above, we have ![]() . As a result, we have
. As a result, we have ![]() . So, we have
. So, we have ![]() . As a result, our answer is
. As a result, our answer is ![]() .
.
Solution By BladeRunnerAUG (Fanyuchen20020715). Edited by bgn4493.
Solution 4
Note that the tangents to the circles at ![]() and
and ![]() intersect at a point
intersect at a point ![]() on
on ![]() by radical axis theorem. Since
by radical axis theorem. Since ![]() and
and ![]() , we have
, we have
![]() so
so ![]() is cyclic.
is cyclic.
But if ![]() is the center of
is the center of ![]() , clearly
, clearly ![]() is cyclic with diameter
is cyclic with diameter ![]() , so
, so ![]() implies that
implies that ![]() is the midpoint of
is the midpoint of ![]() . Then, by power of point
. Then, by power of point ![]() ,
, ![]() whereas it is given that
whereas it is given that ![]() . Thus
. Thus ![]() so
so ![]() , i.e.
, i.e. ![]() and the answer is
and the answer is ![]() .
.
Solution 5
Connect ![]() , since
, since ![]() , so
, so ![]() then, so
then, so ![]() are concyclic
are concyclic
We let ![]() , it is clear that
, it is clear that ![]() , which leads to the conclusion
, which leads to the conclusion ![]() which tells
which tells ![]() is the midpoint of
is the midpoint of ![]()
Then it is clear, ![]() , the answer is
, the answer is ![]()
~bluesoul
Solution 6(calculationless)
![]() by power of a point. Also,
by power of a point. Also, ![]() , so
, so ![]() and
and ![]() are solutions to the quadratic
are solutions to the quadratic ![]() so
so ![]() and
and ![]() is
is ![]() in some order. Now, because we want
in some order. Now, because we want ![]() and it is known to be rational, we can guess that
and it is known to be rational, we can guess that ![]() is irrational or the problem would simply ask for
is irrational or the problem would simply ask for ![]() .
. ![]() , and chances are low that
, and chances are low that ![]() is some number with a square root plus or minus
is some number with a square root plus or minus ![]() to cancel out the
to cancel out the ![]() in
in ![]() , so one can see that
, so one can see that ![]() is most likely to be
is most likely to be ![]() , and our answer is
, and our answer is ![]()
Note : If our answer is correct, then ![]() , which made Q the midpoint of XY, a feature that occurs often in AIME problems, so that again made our answer probable, and even if it's wrong, it's still the same as leaving it blank because it's a AIME problem. ~ddk001
, which made Q the midpoint of XY, a feature that occurs often in AIME problems, so that again made our answer probable, and even if it's wrong, it's still the same as leaving it blank because it's a AIME problem. ~ddk001
See Also
| 2019 AIME I (Problems • Answer Key • Resources) | ||
| Preceded by Problem 14 |
Followed by Last Problem | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()