Difference between revisions of "1971 Canadian MO Problems/Problem 1"
m (wikified) |
|||
| Line 5: | Line 5: | ||
== Solution == | == Solution == | ||
| − | First, extend <math>\displaystyle CO</math> to meet the circle at <math>\displaystyle P.</math> Let the radius be <math>\displaystyle r.</math> Applying Power of a Point, | + | First, extend <math>\displaystyle CO</math> to meet the circle at <math>\displaystyle P.</math> Let the radius be <math>\displaystyle r.</math> Applying [[Power of a Point]], |
<math>\displaystyle (EP)(CE)=(BE)(ED)</math> and <math>\displaystyle 2r-1=15.</math> Hence, <math>\displaystyle r=8.</math> | <math>\displaystyle (EP)(CE)=(BE)(ED)</math> and <math>\displaystyle 2r-1=15.</math> Hence, <math>\displaystyle r=8.</math> | ||
Revision as of 16:16, 26 July 2006
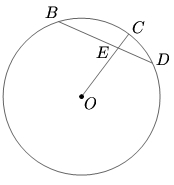
Problem
![]() is a chord of a circle such that
is a chord of a circle such that ![]() and
and ![]() Let
Let ![]() be the center of the circle. Join
be the center of the circle. Join ![]() and extend
and extend ![]() to cut the circle at
to cut the circle at ![]() Given
Given ![]() find the radius of the circle
find the radius of the circle
Solution
First, extend ![]() to meet the circle at
to meet the circle at ![]() Let the radius be
Let the radius be ![]() Applying Power of a Point,
Applying Power of a Point,
![]() and
and ![]() Hence,
Hence, ![]()