Difference between revisions of "1993 AIME Problems/Problem 14"
(→Solution) |
(→Solution 1) |
||
| (7 intermediate revisions by 4 users not shown) | |||
| Line 2: | Line 2: | ||
A rectangle that is inscribed in a larger rectangle (with one vertex on each side) is called unstuck if it is possible to rotate (however slightly) the smaller rectangle about its center within the confines of the larger. Of all the rectangles that can be inscribed unstuck in a 6 by 8 rectangle, the smallest perimeter has the form <math>\sqrt{N}\,</math>, for a positive integer <math>N\,</math>. Find <math>N\,</math>. | A rectangle that is inscribed in a larger rectangle (with one vertex on each side) is called unstuck if it is possible to rotate (however slightly) the smaller rectangle about its center within the confines of the larger. Of all the rectangles that can be inscribed unstuck in a 6 by 8 rectangle, the smallest perimeter has the form <math>\sqrt{N}\,</math>, for a positive integer <math>N\,</math>. Find <math>N\,</math>. | ||
| − | == Solution == | + | == Solution 1 == |
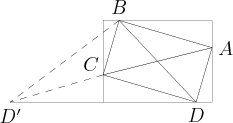
| − | + | Put the rectangle on the coordinate plane so its vertices are at <math>(\pm4,\pm3)</math>, for all four combinations of positive and negative. Then by symmetry, the other rectangle is also centered at the origin, <math>O</math>. | |
| − | |||
| − | |||
Note that such a rectangle is unstuck if its four vertices are in or on the edge of all four quadrants, and it is not the same rectangle as the big one. Let the four vertices of this rectangle be <math>A(4,y)</math>, <math>B(-x,3)</math>, <math>C(-4,-y)</math> and <math>D(x,-3)</math> for nonnegative <math>x,y</math>. Then this is a rectangle, so <math>OA=OB</math>, or <math>16+y^2=9+x^2</math>, so <math>x^2=y^2+7</math>. | Note that such a rectangle is unstuck if its four vertices are in or on the edge of all four quadrants, and it is not the same rectangle as the big one. Let the four vertices of this rectangle be <math>A(4,y)</math>, <math>B(-x,3)</math>, <math>C(-4,-y)</math> and <math>D(x,-3)</math> for nonnegative <math>x,y</math>. Then this is a rectangle, so <math>OA=OB</math>, or <math>16+y^2=9+x^2</math>, so <math>x^2=y^2+7</math>. | ||
| Line 15: | Line 13: | ||
If <math>y</math> is positive, it can be decreased to <math>y'<y</math>. This causes <math>x</math> to decrease as well, to <math>x'</math>, where <math>x'^2=y'^2+7</math> and <math>x'</math> is still positive. If <math>B</math> and <math>D'</math> are held in place as everything else moves, then <math>C</math> moves <math>(y-y')</math> units up and <math>(x-x')</math> units left to <math>C'</math>, which must lie within <math>\triangle BCD'</math>. Then we must have <math>BC'+C'D'<BC+CD'</math>, and the perimeter of the rectangle is decreased. Therefore, the minimum perimeter must occur with <math>y=0</math>, so <math>x=\sqrt7</math>. | If <math>y</math> is positive, it can be decreased to <math>y'<y</math>. This causes <math>x</math> to decrease as well, to <math>x'</math>, where <math>x'^2=y'^2+7</math> and <math>x'</math> is still positive. If <math>B</math> and <math>D'</math> are held in place as everything else moves, then <math>C</math> moves <math>(y-y')</math> units up and <math>(x-x')</math> units left to <math>C'</math>, which must lie within <math>\triangle BCD'</math>. Then we must have <math>BC'+C'D'<BC+CD'</math>, and the perimeter of the rectangle is decreased. Therefore, the minimum perimeter must occur with <math>y=0</math>, so <math>x=\sqrt7</math>. | ||
| − | By the distance formula, this minimum perimeter is <cmath>2\left(\sqrt{(4-\sqrt7)^2+3^2}+\sqrt{(4+\sqrt7)^2+3^2}\right)=4\left(\sqrt{8-2\sqrt7}+\sqrt{8+2\sqrt7}\right)</cmath> <cmath>=4(\sqrt7-1+\sqrt7+1)=8\sqrt7=\sqrt{448}.</cmath> | + | By the distance formula, this minimum perimeter is <cmath>2\left(\sqrt{(4-\sqrt7)^2+3^2}+\sqrt{(4+\sqrt7)^2+3^2}\right)=4\left(\sqrt{8-2\sqrt7}+\sqrt{8+2\sqrt7}\right)</cmath> <cmath>=4(\sqrt7-1+\sqrt7+1)=8\sqrt7=\sqrt{448}.</cmath> Therefore <math>N</math> would equal <math>\boxed{448}.</math> |
| + | |||
| + | ~minor edit by Yiyj1 and Root three over two | ||
== Solution 2 == | == Solution 2 == | ||
Latest revision as of 09:25, 19 November 2023
Contents
Problem
A rectangle that is inscribed in a larger rectangle (with one vertex on each side) is called unstuck if it is possible to rotate (however slightly) the smaller rectangle about its center within the confines of the larger. Of all the rectangles that can be inscribed unstuck in a 6 by 8 rectangle, the smallest perimeter has the form ![]() , for a positive integer
, for a positive integer ![]() . Find
. Find ![]() .
.
Solution 1
Put the rectangle on the coordinate plane so its vertices are at ![]() , for all four combinations of positive and negative. Then by symmetry, the other rectangle is also centered at the origin,
, for all four combinations of positive and negative. Then by symmetry, the other rectangle is also centered at the origin, ![]() .
.
Note that such a rectangle is unstuck if its four vertices are in or on the edge of all four quadrants, and it is not the same rectangle as the big one. Let the four vertices of this rectangle be ![]() ,
, ![]() ,
, ![]() and
and ![]() for nonnegative
for nonnegative ![]() . Then this is a rectangle, so
. Then this is a rectangle, so ![]() , or
, or ![]() , so
, so ![]() .
.
Reflect ![]() across the side of the rectangle containing
across the side of the rectangle containing ![]() to
to ![]() . Then
. Then ![]() is constant, and the perimeter of the rectangle is equal to
is constant, and the perimeter of the rectangle is equal to ![]() . The midpoint of
. The midpoint of ![]() is
is ![]() , and since
, and since ![]() and
and ![]() ,
, ![]() always lies below
always lies below ![]() .
.
If ![]() is positive, it can be decreased to
is positive, it can be decreased to ![]() . This causes
. This causes ![]() to decrease as well, to
to decrease as well, to ![]() , where
, where ![]() and
and ![]() is still positive. If
is still positive. If ![]() and
and ![]() are held in place as everything else moves, then
are held in place as everything else moves, then ![]() moves
moves ![]() units up and
units up and ![]() units left to
units left to ![]() , which must lie within
, which must lie within ![]() . Then we must have
. Then we must have ![]() , and the perimeter of the rectangle is decreased. Therefore, the minimum perimeter must occur with
, and the perimeter of the rectangle is decreased. Therefore, the minimum perimeter must occur with ![]() , so
, so ![]() .
.
By the distance formula, this minimum perimeter is ![]()
![]() Therefore
Therefore ![]() would equal
would equal ![]()
~minor edit by Yiyj1 and Root three over two
Solution 2
Note that the diagonal of the rectangle with minimum perimeter must have the diagonal along the middle segment of length 8 of the rectangle (any other inscribed rectangle can be rotated a bit, then made smaller; this one can't because then the rectangle cannot be inscribed since its longest diagonal is less than 8 in length). Then since a rectangle must have right angles, we draw a circle of radius 4 around the center of the rectangle. Picking the two midpoints on the sides of length 6 and opposite intersection points on the segments of length 8, we form a rectangle. Let ![]() and
and ![]() be the sides of the rectangle. Then
be the sides of the rectangle. Then ![]() since both are twice the area of the same right triangle, and
since both are twice the area of the same right triangle, and ![]() . So
. So ![]() , so
, so ![]() .
.
See also
| 1993 AIME (Problems • Answer Key • Resources) | ||
| Preceded by Problem 13 |
Followed by Problem 15 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.