1998 AIME Problems/Problem 2
Problem
Find the number of ordered pairs ![]() of positive integers that satisfy
of positive integers that satisfy ![]() and
and ![]() .
.
Contents
Solution
Solution 1
Pick's theorem states that:
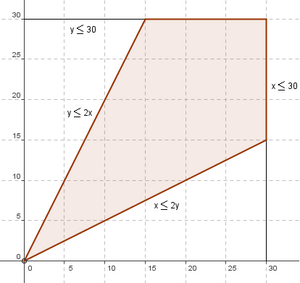
The conditions give us four inequalities: ![]() ,
, ![]() ,
, ![]() ,
, ![]() . These create a quadrilateral, whose area is
. These create a quadrilateral, whose area is ![]() of the 30 by 30 square it is in. A simple way to see this is to note that the two triangles outside of the quadrilateral form half of the area of the 30 by 30 square.
of the 30 by 30 square it is in. A simple way to see this is to note that the two triangles outside of the quadrilateral form half of the area of the 30 by 30 square.
So ![]() .
. ![]() we can calculate by just counting. Ignoring the vertices, the top and right sides have 14 lattice points, and the two diagonals each have 14 lattice points (for the top diagonal, every value of
we can calculate by just counting. Ignoring the vertices, the top and right sides have 14 lattice points, and the two diagonals each have 14 lattice points (for the top diagonal, every value of ![]() corresponds with an integer value of
corresponds with an integer value of ![]() as
as ![]() and vice versa for the bottom, so and there are 14 values for x not counting vertices). Adding the four vertices, there are 60 points on the borders.
and vice versa for the bottom, so and there are 14 values for x not counting vertices). Adding the four vertices, there are 60 points on the borders.
Since the inequalities also include the equals case, we include the boundaries, which gives us ![]() ordered pairs. However, the question asks us for positive integers, so
ordered pairs. However, the question asks us for positive integers, so ![]() doesn't count; hence, the answer is
doesn't count; hence, the answer is ![]() .
.
Solution 2
First, note that all pairs of the form ![]() ,
, ![]() work.
work.
Now, considered the ordered pairs with ![]() , so that
, so that ![]() is automatically satisfied. Since
is automatically satisfied. Since ![]() , there are
, there are ![]() possible values of
possible values of ![]() . Hence, given
. Hence, given ![]() , there are
, there are ![]() values of possible
values of possible ![]() for which
for which ![]() and the above conditions are satisfied. But
and the above conditions are satisfied. But ![]() , so this only works for
, so this only works for ![]() . Thus, there are
. Thus, there are

ordered pairs. For ![]() ,
, ![]() must follow
must follow ![]() . Hence, there are
. Hence, there are ![]() possibilities for
possibilities for ![]() , and there are
, and there are

ordered pairs.
By symmetry, there are also ![]() ordered pairs with
ordered pairs with ![]() and the above criteria satisfied.
and the above criteria satisfied.
Hence, the total is
![]()
Solution 3
![]()
Multiplying both sides by 2 yields:
![]()
Then the two inequalities can be merged to form the following inequality:
![]()
Additionally, we must ensure that ![]()
Therefore we must find pairs ![]() that satisfy the inequality above.
A bit of trial and error and observing patterns leads to the answer
that satisfy the inequality above.
A bit of trial and error and observing patterns leads to the answer ![]() .
.
It should be noted that the cases for ![]() and
and ![]() should be considered separately in order to ensure that
should be considered separately in order to ensure that ![]() .
.
Solution 4 - Unrigorous engineers induction solution
We will try out small cases.
By replacing 60 in this problem with 2, we count only 1 ordered pair. By doing with 4, we count 4 ordered pairs. With 6, we get 7 pairs. With 8 we get 12. By continuing on, and then finding the difference between adjacent terms (1,3,3,5,5,...). We suspect that if 60 was replaced with 2n, we will find 1+3+3+5+5+7+7 ...., where there will be n terms. Thus, our answer is 1+3+3+5+5.... 29+29+31 = 16*30 = 480.
-Alexlikemath
Solution 5 - Counting Head on
Notice ![]() and
and ![]() both must be equal or less than 30. The inequalities given have no complicated qualities. We can recompile them by understanding: Two times the larger integer will also be larger than the smaller integer; Two times the smaller integer is greater or equal to the greater integer if and only if the greater integer is less or equal to the double of the smaller integer. Knowing this, we create a chart. We will first solve without order, then multiply pairs by 2 at the end.
both must be equal or less than 30. The inequalities given have no complicated qualities. We can recompile them by understanding: Two times the larger integer will also be larger than the smaller integer; Two times the smaller integer is greater or equal to the greater integer if and only if the greater integer is less or equal to the double of the smaller integer. Knowing this, we create a chart. We will first solve without order, then multiply pairs by 2 at the end. ![]() can be 1-30, so we'll start with 1. The only possible value for
can be 1-30, so we'll start with 1. The only possible value for ![]() is 1. For
is 1. For ![]() ,
, ![]() can be 2-4. For
can be 2-4. For ![]() ,
, ![]() can be 3-6. There is an obvious pattern here. For every integer after 1, the possible values for
can be 3-6. There is an obvious pattern here. For every integer after 1, the possible values for ![]() will be numbers
will be numbers ![]() -
-![]() . This predictably ends at
. This predictably ends at ![]() because
because ![]() will reach 30. When
will reach 30. When ![]() , then the number of possible values of
, then the number of possible values of ![]() will begin to drop again, equaling the amount when
will begin to drop again, equaling the amount when ![]() . Then when we finally sum the group together, for
. Then when we finally sum the group together, for ![]() to
to ![]() there are 104 pairs with 2 distinct values, and 13 values with congruent values. These will not be multiplied by 2 later on.
there are 104 pairs with 2 distinct values, and 13 values with congruent values. These will not be multiplied by 2 later on. ![]() to
to ![]() gives the same amount. Then
gives the same amount. Then ![]() and
and ![]() gives 16 and 2 values respectively, with two congruent values each. Finally,
gives 16 and 2 values respectively, with two congruent values each. Finally, ![]() and
and ![]() give 3 and 1 respectively.
give 3 and 1 respectively.
Sum them together and you will get 480.
-jackshi2006
See also
| 1998 AIME (Problems • Answer Key • Resources) | ||
| Preceded by Problem 1 |
Followed by Problem 3 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.