Difference between revisions of "2003 AMC 8 Problems/Problem 24"
Glowinglol (talk | contribs) (Created page with "The distance from X remains constant for the semicircle, so the first part of the graph has to be a straight line. Then, the line gets closer, and then farther away from X. So, (...") |
Icematrix2 (talk | contribs) |
||
| (6 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | The distance from X | + | ==Problem== |
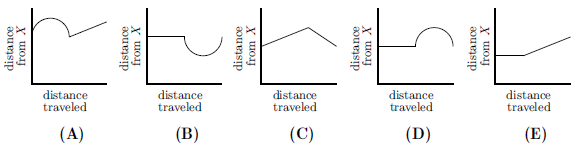
| + | A ship travels from point <math>A</math> to point <math>B</math> along a semicircular path, centered at Island <math>X</math>. Then it travels along a straight path from <math>B</math> to <math>C</math>. Which of these graphs best shows the ship's distance from Island <math>X</math> as it moves along its course? | ||
| + | |||
| + | <asy>size(150); | ||
| + | pair X=origin, A=(-5,0), B=(5,0), C=(0,5); | ||
| + | draw(Arc(X, 5, 180, 360)^^B--C); | ||
| + | dot(X); | ||
| + | label("$X$", X, NE); | ||
| + | label("$C$", C, N); | ||
| + | label("$B$", B, E); | ||
| + | label("$A$", A, W); | ||
| + | </asy> | ||
| + | |||
| + | <center> | ||
| + | [[Image:2003amc8prob24ans.png|800px]] | ||
| + | </center> | ||
| + | |||
| + | ==Solution== | ||
| + | |||
| + | The distance from Island <math>\text{X}</math> to any point on the semicircle will always be constant. On the graph, this will represent a straight line. The distance between Island <math>\text{X}</math> and line <math>\text{BC}</math> will not be constant though. We can easily prove that the distance between <math>\text{X}</math> and line <math>\text{BC}</math> will represent a curve. As the ship travels from <math>B</math> to <math>C</math>, the distance between the ship and Island <math>X</math> will first decrease until it reaches the point <math>Y</math> so that <math>\overline{XY}</math> is perpendicular to <math>\overline{BC}</math>, and then increase afterwards. Hence the answer choice that fits them all is <math>\boxed{\text{(B)}}</math>. | ||
| + | |||
| + | ==See Also== | ||
| + | {{AMC8 box|year=2003|num-b=23|num-a=25}} | ||
| + | |||
| + | [[Category:Introductory Geometry Problems]] | ||
| + | {{MAA Notice}} | ||
Revision as of 21:36, 9 October 2020
Problem
A ship travels from point 
to point 
along a semicircular path, centered at Island 
. Then it travels along a straight path from to 
. Which of these graphs best shows the ship's distance from Island as it moves along its course?
![[asy]size(150); pair X=origin, A=(-5,0), B=(5,0), C=(0,5); draw(Arc(X, 5, 180, 360)^^B--C); dot(X); label("$X$", X, NE); label("$C$", C, N); label("$B$", B, E); label("$A$", A, W); [/asy]](http://latex.artofproblemsolving.com/9/1/9/91933f8be27c24174af480d964c31782da9f3bb4.png)
Solution
The distance from Island 
to any point on the semicircle will always be constant. On the graph, this will represent a straight line. The distance between Island and line 
will not be constant though. We can easily prove that the distance between and line will represent a curve. As the ship travels from to , the distance between the ship and Island will first decrease until it reaches the point 
so that 
is perpendicular to 
, and then increase afterwards. Hence the answer choice that fits them all is 
.
See Also
| 2003 AMC 8 (Problems • Answer Key • Resources) | ||
| Preceded by Problem 23 |
Followed by Problem 25 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AJHSME/AMC 8 Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. 
