2005 AIME II Problems/Problem 15
Contents
Problem
Let ![]() and
and ![]() denote the circles
denote the circles ![]() and
and ![]() respectively. Let
respectively. Let ![]() be the smallest positive value of
be the smallest positive value of ![]() for which the line
for which the line ![]() contains the center of a circle that is externally tangent to
contains the center of a circle that is externally tangent to ![]() and internally tangent to
and internally tangent to ![]() Given that
Given that ![]() where
where ![]() and
and ![]() are relatively prime integers, find
are relatively prime integers, find ![]()
Solution 1
Rewrite the given equations as ![]() and
and ![]() .
.
Let ![]() have center
have center ![]() and radius
and radius ![]() . Now, if two circles with radii
. Now, if two circles with radii ![]() and
and ![]() are externally tangent, then the distance between their centers is
are externally tangent, then the distance between their centers is ![]() , and if they are internally tangent, it is
, and if they are internally tangent, it is ![]() . So we have
. So we have

Solving for ![]() in both equations and setting them equal, then simplifying, yields
in both equations and setting them equal, then simplifying, yields

Squaring again and canceling yields ![]()
So the locus of points that can be the center of the circle with the desired properties is an ellipse.
![[asy] size(220); pointpen = black; pen d = linewidth(0.7); pathpen = d; pair A = (-5, 12), B = (5, 12), C = (0, 0); D(CR(A,16));D(CR(B,4));D(shift((0,12)) * yscale(3^.5 / 2) * CR(C,10), linetype("2 2") + d + red); D((0,30)--(0,-10),Arrows(4));D((15,0)--(-25,0),Arrows(4));D((0,0)--MP("y=ax",(14,14 * (69/100)^.5),E),EndArrow(4)); void bluecirc (real x) { pair P = (x, (3 * (25 - x^2 / 4))^.5 + 12); dot(P, blue); D(CR(P, ((P.x - 5)^2 + (P.y - 12)^2)^.5 - 4) , blue + d + linetype("4 4")); } bluecirc(-9.2); bluecirc(-4); bluecirc(3); [/asy]](http://latex.artofproblemsolving.com/3/9/5/3952f7611dcec95c9d68289eb69eb74de86b62bc.png)
Since the center lies on the line ![]() , we substitute for
, we substitute for ![]() and expand:
and expand:
![]()
We want the value of ![]() that makes the line
that makes the line ![]() tangent to the ellipse, which will mean that for that choice of
tangent to the ellipse, which will mean that for that choice of ![]() there is only one solution to the most recent equation. But a quadratic has one solution iff its discriminant is
there is only one solution to the most recent equation. But a quadratic has one solution iff its discriminant is ![]() , so
, so ![]() .
.
Solving yields ![]() , so the answer is
, so the answer is ![]() .
.
Solution 2
As above, we rewrite the equations as ![]() and
and ![]() . Let
. Let ![]() and
and ![]() . If a circle with center
. If a circle with center ![]() and radius
and radius ![]() is externally tangent to
is externally tangent to ![]() and internally tangent to
and internally tangent to ![]() , then
, then ![]() and
and ![]() . Therefore,
. Therefore, ![]() . In particular, the locus of points
. In particular, the locus of points ![]() that can be centers of circles must be an ellipse with foci
that can be centers of circles must be an ellipse with foci ![]() and
and ![]() and major axis
and major axis ![]() .
.
Clearly, the minimum value of the slope ![]() will occur when the line
will occur when the line ![]() is tangent to this ellipse. Suppose that this point of tangency is denoted by
is tangent to this ellipse. Suppose that this point of tangency is denoted by ![]() , and the line
, and the line ![]() is denoted by
is denoted by ![]() . Then we reflect the ellipse over
. Then we reflect the ellipse over ![]() to a new ellipse with foci
to a new ellipse with foci ![]() and
and ![]() as shown below.
as shown below.
![[asy] size(220); pair F1 = (-5, 12), F2 = (5, 12),C=(0,12); draw(circle(F1,16)); draw(circle(F2,4)); draw(ellipse(C,10,5*sqrt(3))); xaxis("$x$",Arrows); yaxis("$y$",Arrows); dot(F1^^F2^^C); real l(real x) {return sqrt(69)*x/10;} path g=graph(l,-7,14); draw(g); draw(reflect((0,0),(10,l(10)))*ellipse(C,10,5*sqrt(3))); pair T=intersectionpoint(ellipse(C,10,5*sqrt(3)),(0,0)--(10,l(10))); dot(T); pair F1P=reflect((0,0),(10,l(10)))*F1; pair F2P=reflect((0,0),(10,l(10)))*F2; dot(F1P^^F2P); dot((0,0)); label("$F_1$",F1,N,fontsize(9)); label("$F_2$",F2,N,fontsize(9)); label("$F_1'$",F1P,SE,fontsize(9)); label("$F_2'$",F2P,SE,fontsize(9)); label("$O$",(0,0),NW,fontsize(9)); label("$\ell$",(13,l(13)),SE,fontsize(9)); label("$T$",T,NW,fontsize(9)); draw((0,0)--F1--F2--F2P--F1P--cycle); draw(F1--F2P^^F2--F1P); [/asy]](http://latex.artofproblemsolving.com/3/9/f/39f7436c9b561798a9afaf9bddc9c97fd6de020d.png)
By the reflection property of ellipses (i.e., the angle of incidence to a tangent line is equal to the angle of reflection for any path that travels between the foci), we know that ![]() ,
, ![]() , and
, and ![]() are collinear, and similarly,
are collinear, and similarly, ![]() ,
, ![]() and
and ![]() are collinear. Therefore,
are collinear. Therefore, ![]() is a pentagon with
is a pentagon with ![]() ,
, ![]() , and
, and ![]() . Note that
. Note that ![]() bisects
bisects ![]() . We can bisect this angle by bisecting
. We can bisect this angle by bisecting ![]() and
and ![]() separately.
separately.
We proceed using complex numbers. Triangle ![]() is isosceles with side lengths
is isosceles with side lengths ![]() . The height of this from the base of
. The height of this from the base of ![]() is
is ![]() . Therefore, the complex number
. Therefore, the complex number ![]() represents the bisection of
represents the bisection of ![]() .
.
Similarly, using the 5-12-13 triangles, we easily see that ![]() represents the bisection of the angle
represents the bisection of the angle ![]() . Therefore, we can add these two angles together by multiplying the complex numbers, finding
. Therefore, we can add these two angles together by multiplying the complex numbers, finding
![]() Now the point
Now the point ![]() is given by the complex number
is given by the complex number ![]() . Therefore, to find a point on line
. Therefore, to find a point on line ![]() , we simply subtract
, we simply subtract ![]() , which is the same as multiplying
, which is the same as multiplying ![]() by the conjugate of
by the conjugate of ![]() . We find
. We find
![]() In particular, note that the tangent of the argument of this complex number is
In particular, note that the tangent of the argument of this complex number is ![]() , which must be the slope of the tangent line. Hence
, which must be the slope of the tangent line. Hence ![]() , and the answer is
, and the answer is ![]() .
.
Solution 3
We use the same reflection as in Solution 2. As ![]() , we know that
, we know that ![]() is isosceles. Hence
is isosceles. Hence ![]() . But by symmetry, we also know that
. But by symmetry, we also know that ![]() . Hence
. Hence ![]() . In particular, as
. In particular, as ![]() , this implies that
, this implies that ![]() , and
, and ![]() are concyclic.
are concyclic.
Let ![]() be the intersection of
be the intersection of ![]() with the
with the ![]() -axis. As
-axis. As ![]() is parallel to the
is parallel to the ![]() -axis, we know that
-axis, we know that ![]() But
But ![]() By the fact that
By the fact that ![]() is cyclic,
is cyclic, ![]() Therefore, combining (1), (2), and (3), we find that
Therefore, combining (1), (2), and (3), we find that
![]()
By symmetry, we also know that
![]() Therefore, (4) and (5) show by AA similarity that
Therefore, (4) and (5) show by AA similarity that ![]() . Therefore,
. Therefore, ![]() .
.
Now as ![]() , we know that
, we know that ![]() is isosceles, and as
is isosceles, and as ![]() , we can drop an altitude to
, we can drop an altitude to ![]() to easily find that
to easily find that ![]() . Therefore,
. Therefore, ![]() , which is the desired slope, must also be
, which is the desired slope, must also be ![]() . As before, we conclude that the answer is
. As before, we conclude that the answer is ![]() .
.
Solution 4
First, rewrite the equations for the circles as ![]() and
and ![]() .
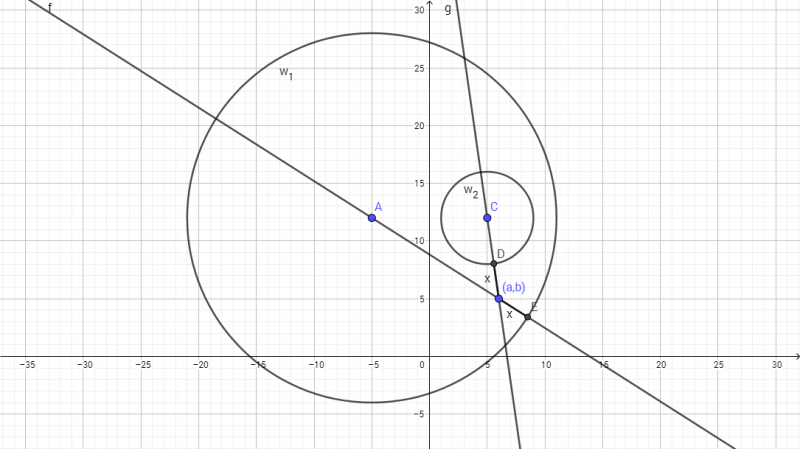
Then, choose a point
.
Then, choose a point ![]() that is a distance of
that is a distance of ![]() from both circles. Use the distance formula between
from both circles. Use the distance formula between ![]() and each of
and each of ![]() and
and ![]() (in the diagram above). The distances, as can be seen in the diagram above are
(in the diagram above). The distances, as can be seen in the diagram above are ![]() and
and ![]() , respectively.
, respectively.
![]()
![]() Subtracting the first equation from the second gives
Subtracting the first equation from the second gives ![]() Substituting this into the first equation gives
Substituting this into the first equation gives
![]()
![]() Now, instead of converting this to the equation of an eclipse, solve for
Now, instead of converting this to the equation of an eclipse, solve for ![]() and then divide by
and then divide by ![]() .
.
![]() We take the smaller root to minimize
We take the smaller root to minimize ![]() .
.
![]() Now, let
Now, let ![]() . This way,
. This way, ![]() .
Substitute this in.
.
Substitute this in. ![]() Then, take the derivative of this and set it to 0 to find the minimum value.
Then, take the derivative of this and set it to 0 to find the minimum value.
![]() Then, use this value of
Then, use this value of ![]() to find the minimum of
to find the minimum of ![]() to get
to get 
Solution 5 (probably fastest)
Like before, notice that the distances from the centers of the given circles to the desired center are ![]() and
and ![]() , which add up to
, which add up to ![]() . This means that the possible centers of the third circle lie on an ellipse with foci
. This means that the possible centers of the third circle lie on an ellipse with foci ![]() and
and ![]() . Using the fact that the sum of the distances from the foci is
. Using the fact that the sum of the distances from the foci is ![]() , we find that the semi-major axis has length
, we find that the semi-major axis has length ![]() and the semi-minor axis has length
and the semi-minor axis has length ![]() . Therefore, the equation of the ellipse is
. Therefore, the equation of the ellipse is ![]() where the numbers
where the numbers ![]() and
and ![]() come from
come from ![]() and
and ![]() respectively.
respectively.
We proceed to find ![]() using the same method as Solution 1.
using the same method as Solution 1.
See also
| 2005 AIME II (Problems • Answer Key • Resources) | ||
| Preceded by Problem 14 |
Followed by Last Question | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.