Difference between revisions of "2006 AMC 12A Problems/Problem 22"
m (minor edit) |
|||
| (12 intermediate revisions by 6 users not shown) | |||
| Line 1: | Line 1: | ||
== Problem == | == Problem == | ||
| + | A [[circle]] of [[radius]] <math>r</math> is [[concentric]] with and outside a [[regular polygon | regular]] [[hexagon]] of side length <math>2</math>. The [[probability]] that three entire sides of hexagon are visible from a randomly chosen point on the circle is <math>1/2</math>. What is <math>r</math>? | ||
| − | + | <math> \mathrm{(A) \ } 2\sqrt{2}+2\sqrt{3}\qquad \mathrm{(B) \ } 3\sqrt{3}+\sqrt{2}\qquad \mathrm{(C) \ } 2\sqrt{6}+\sqrt{3}\qquad \rm{(D) \ } 3\sqrt{2}+\sqrt{6}\qquad \mathrm{(E) \ } 6\sqrt{2}-\sqrt{3}</math> | |
| − | <math> \ | + | == Solution == |
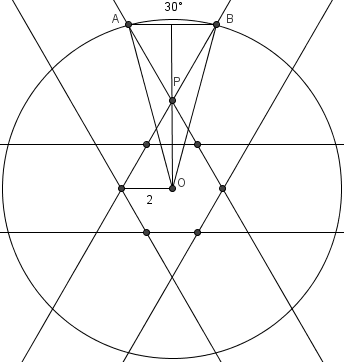
| + | Project any two non-adjacent and non-opposite sides of the [[hexagon]] to the [[circle]]; the [[arc]] between the two points formed is the location where all three sides of the hexagon can be fully viewed. Since there are six such pairs of sides, there are six arcs. The probability of choosing a point is <math>1 / 2</math>, or if the total arc degree measures add up to <math>\frac{1}{2} \cdot 360^{\circ} = 180^{\circ}</math>. Each arc must equal <math>\frac{180^{\circ}}{6} = 30^\mathrm{\circ}</math>. | ||
| − | + | [[Image:2006_12A_AMC-22.png]] | |
| − | == | + | Call the center <math>O</math>, and the two endpoints of the arc <math>A</math> and <math>B</math>, so <math>\angle AOB = 30^{\circ}</math>. Let <math>P</math> be the intersections of the projections of the sides of the hexagon corresponding to <math>\overline{AB}</math>. Notice that <math>\triangle APO</math> is an [[isosceles triangle]]: <math>\angle AOP = 15^{\circ}</math> and <math>\angle OAP = OAB - 60^{\circ} = \frac{180^{\circ}-30^{\circ}}{2} - 60^{\circ} = 15^{\circ}</math>. Since <math>OA</math> is a radius and <math>OP</math> can be found in terms of a side of the hexagon, we are almost done. |
| + | |||
| + | If we draw the altitude of <math>APO</math> from <math>P</math>, then we get a [[right triangle]]. Using simple trigonometry, <math>\cos 15^{\circ} = \frac{\frac{r}{2}}{2\sqrt{3}} = \frac{r}{4\sqrt{3}}</math>. | ||
| + | |||
| + | Since <math>\cos 15^{\circ} = \cos (45^{\circ} - 30^{\circ}) = \frac{\sqrt{6} + \sqrt{2}}{4}</math>, we get <math>r = \left(\frac{\sqrt{6} + \sqrt{2}}{4}\right) \cdot 4\sqrt{3} = 3\sqrt{2} + \sqrt{6} \Rightarrow \mathrm{(D)}</math>. | ||
| + | |||
| + | == See Also == | ||
| + | {{AMC12 box|year=2006|ab=A|num-b=21|num-a=23}} | ||
| + | {{MAA Notice}} | ||
| − | + | [[Category:Intermediate Geometry Problems]] | |
| − | |||
Revision as of 01:01, 19 October 2020
Problem
A circle of radius ![]() is concentric with and outside a regular hexagon of side length
is concentric with and outside a regular hexagon of side length ![]() . The probability that three entire sides of hexagon are visible from a randomly chosen point on the circle is
. The probability that three entire sides of hexagon are visible from a randomly chosen point on the circle is ![]() . What is
. What is ![]() ?
?
![]()
Solution
Project any two non-adjacent and non-opposite sides of the hexagon to the circle; the arc between the two points formed is the location where all three sides of the hexagon can be fully viewed. Since there are six such pairs of sides, there are six arcs. The probability of choosing a point is ![]() , or if the total arc degree measures add up to
, or if the total arc degree measures add up to ![]() . Each arc must equal
. Each arc must equal ![]() .
.
Call the center ![]() , and the two endpoints of the arc
, and the two endpoints of the arc ![]() and
and ![]() , so
, so ![]() . Let
. Let ![]() be the intersections of the projections of the sides of the hexagon corresponding to
be the intersections of the projections of the sides of the hexagon corresponding to ![]() . Notice that
. Notice that ![]() is an isosceles triangle:
is an isosceles triangle: ![]() and
and ![]() . Since
. Since ![]() is a radius and
is a radius and ![]() can be found in terms of a side of the hexagon, we are almost done.
can be found in terms of a side of the hexagon, we are almost done.
If we draw the altitude of ![]() from
from ![]() , then we get a right triangle. Using simple trigonometry,
, then we get a right triangle. Using simple trigonometry, ![]() .
.
Since ![]() , we get
, we get  .
.
See Also
| 2006 AMC 12A (Problems • Answer Key • Resources) | |
| Preceded by Problem 21 |
Followed by Problem 23 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.