Difference between revisions of "2011 AIME I Problems/Problem 13"
JoetheFixer (talk | contribs) (→Solution 2) |
(→Solution 2) |
||
| (21 intermediate revisions by 10 users not shown) | |||
| Line 1: | Line 1: | ||
== Problem == | == Problem == | ||
| − | A cube with side length 10 is suspended above a plane. The vertex closest to the plane is labeled <math>A</math>. The three vertices adjacent to vertex <math>A</math> are at heights 10, 11, and 12 above the plane. The distance from vertex <math>A</math> to the plane can be expressed as <math> \frac{r-\sqrt{s}}{t}</math>, where <math>r</math>, <math>s</math>, and <math>t</math> are positive integers | + | A cube with side length 10 is suspended above a plane. The vertex closest to the plane is labeled <math>A</math>. The three vertices adjacent to vertex <math>A</math> are at heights 10, 11, and 12 above the plane. The distance from vertex <math>A</math> to the plane can be expressed as <math> \frac{r-\sqrt{s}}{t}</math>, where <math>r</math>, <math>s</math>, and <math>t</math> are positive integers. Find <math>r+s+t</math>. |
| − | ==Solution== | + | ==Solution 1== |
| − | Set the cube at the origin with the three vertices along the axes and the plane equal to <math>ax+by+cz+d=0</math>, where <math>a^2+b^2+c^2=1</math>. | + | Set the cube at the origin with the three vertices along the axes and the plane equal to <math>ax+by+cz+d=0</math>, where <math>a^2+b^2+c^2=1</math>. The distance from a point <math>(X,Y,Z)</math> to a plane with equation <math>Ax+By+Cz+D=0</math> is |
| + | <cmath>\frac{AX+BY+CZ+D}{\sqrt{A^2+B^2+C^2}},</cmath> | ||
| + | so the (directed) distance from any point <math>(x,y,z)</math> to the plane is <math>ax+by+cz+d</math>. So, by looking at the three vertices, we have <math>10a+d=10, 10b+d=11, 10c+d=12</math>, and by rearranging and summing, <cmath>(10-d)^2+(11-d)^2+(12-d)^2= 100\cdot(a^2+b^2+c^2)=100.</cmath> | ||
| − | Solving the equation is easier if we substitute <math>11-d=y</math>, to get <math>3y^2+2=100</math>, or <math>y=\sqrt {98/3}</math>. The distance from the origin to the plane is simply d, which is equal to <math>11-\sqrt{98/3} =(33-\sqrt{294})/3</math>, so <math>33+294+3=330</math> | + | Solving the equation is easier if we substitute <math>11-d=y</math>, to get <math>3y^2+2=100</math>, or <math>y=\sqrt {98/3}</math>. The distance from the origin to the plane is simply <math>d</math>, which is equal to <math>11-\sqrt{98/3} =(33-\sqrt{294})/3</math>, so <math>33+294+3=\boxed{330}</math>. |
==Solution 2== | ==Solution 2== | ||
| − | + | Let the vertices with distance <math>10,11,12</math> be <math>B,C,D</math>, respectively. An equilateral triangle <math>\triangle BCD</math> is formed with side length <math>10\sqrt{2}</math>. We care only about the <math>z</math> coordinate: <math>B=10,C=11,D=12</math>. It is well known that the centroid of a triangle is the average of the coordinates of its three vertices, so <math>\text{centroid}=(10+11+12)/3=11</math>. Designate the midpoint of <math>BD</math> as <math>M</math>. Notice that median <math>CM</math> is parallel to the plane because the <math>\text{centroid}</math> and vertex <math>C</math> have the same <math>z</math> coordinate, <math>11</math>, and the median contains <math>C</math> and the <math>\text{centroid}</math>. We seek the angle <math>\theta</math> of the line:<math>(1)</math> through the centroid <math>(2)</math> perpendicular to the plane formed by <math>\triangle BCD</math>, <math>(3)</math> with the plane under the cube. Since the median is parallel to the plane, this orthogonal line is also perpendicular <math>\textit{in slope}</math> to <math>BD</math>. Since <math>BD</math> makes a <math>2-14-10\sqrt{2}</math> right triangle, the orthogonal line makes the same right triangle rotated <math>90^\circ</math>. Therefore, <math>\sin\theta=\frac{14}{10\sqrt{2}}=\frac{7\sqrt{2}}{10}</math>. | |
| + | |||
| + | It is also known that the centroid of <math>\triangle BCD</math> is a third of the way between vertex <math>A</math> and <math>H</math>, the vertex farthest from the plane. Since <math>AH</math> is a diagonal of the cube, <math>AH=10\sqrt{3}</math>. So the distance from the <math>\text{centroid}</math> to <math>A</math> is <math>10/\sqrt{3}</math>. So, the <math>\Delta z</math> from <math>A</math> to the centroid is <math>\frac{10}{\sqrt{3}}\sin\theta=\frac{10}{\sqrt{3}}\left(\frac{7\sqrt{2}}{10}\right)=\frac{7\sqrt{6}}{3}</math>. | ||
| + | |||
| + | Thus the distance from <math>A</math> to the plane is <math>11-\frac{7\sqrt{6}}{3}=\frac{33-7\sqrt{6}}{3}=\frac{33-\sqrt{294}}{3}</math>, and <math>33+294+3=\boxed{330}</math>. | ||
| + | |||
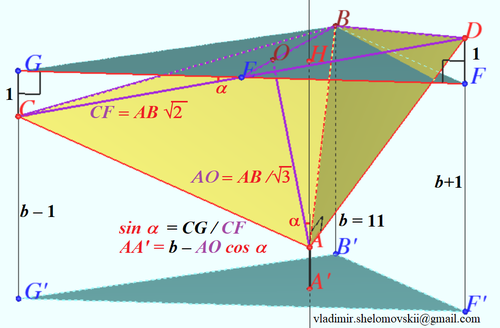
| + | ==Solution 3== | ||
| + | [[File:2011 AIME I 13.png|500px]] | ||
| + | |||
| + | ==Video Solution== | ||
| + | https://youtube.com/watch?v=Wi-aqv8Ron0 | ||
== See also == | == See also == | ||
{{AIME box|year=2011|n=I|num-b=12|num-a=14}} | {{AIME box|year=2011|n=I|num-b=12|num-a=14}} | ||
{{MAA Notice}} | {{MAA Notice}} | ||
| + | [[Category:Intermediate Geometry Problems]] | ||
| + | [[Category:3D Geometry Problems]] | ||
Latest revision as of 11:37, 8 September 2022
Problem
A cube with side length 10 is suspended above a plane. The vertex closest to the plane is labeled ![]() . The three vertices adjacent to vertex
. The three vertices adjacent to vertex ![]() are at heights 10, 11, and 12 above the plane. The distance from vertex
are at heights 10, 11, and 12 above the plane. The distance from vertex ![]() to the plane can be expressed as
to the plane can be expressed as ![]() , where
, where ![]() ,
, ![]() , and
, and ![]() are positive integers. Find
are positive integers. Find ![]() .
.
Solution 1
Set the cube at the origin with the three vertices along the axes and the plane equal to ![]() , where
, where ![]() . The distance from a point
. The distance from a point ![]() to a plane with equation
to a plane with equation ![]() is
is
![]() so the (directed) distance from any point
so the (directed) distance from any point ![]() to the plane is
to the plane is ![]() . So, by looking at the three vertices, we have
. So, by looking at the three vertices, we have ![]() , and by rearranging and summing,
, and by rearranging and summing, ![]()
Solving the equation is easier if we substitute ![]() , to get
, to get ![]() , or
, or ![]() . The distance from the origin to the plane is simply
. The distance from the origin to the plane is simply ![]() , which is equal to
, which is equal to ![]() , so
, so ![]() .
.
Solution 2
Let the vertices with distance ![]() be
be ![]() , respectively. An equilateral triangle
, respectively. An equilateral triangle ![]() is formed with side length
is formed with side length ![]() . We care only about the
. We care only about the ![]() coordinate:
coordinate: ![]() . It is well known that the centroid of a triangle is the average of the coordinates of its three vertices, so
. It is well known that the centroid of a triangle is the average of the coordinates of its three vertices, so ![]() . Designate the midpoint of
. Designate the midpoint of ![]() as
as ![]() . Notice that median
. Notice that median ![]() is parallel to the plane because the
is parallel to the plane because the ![]() and vertex
and vertex ![]() have the same
have the same ![]() coordinate,
coordinate, ![]() , and the median contains
, and the median contains ![]() and the
and the ![]() . We seek the angle
. We seek the angle ![]() of the line:
of the line:![]() through the centroid
through the centroid ![]() perpendicular to the plane formed by
perpendicular to the plane formed by ![]() ,
, ![]() with the plane under the cube. Since the median is parallel to the plane, this orthogonal line is also perpendicular
with the plane under the cube. Since the median is parallel to the plane, this orthogonal line is also perpendicular ![]() to
to ![]() . Since
. Since ![]() makes a
makes a ![]() right triangle, the orthogonal line makes the same right triangle rotated
right triangle, the orthogonal line makes the same right triangle rotated ![]() . Therefore,
. Therefore, ![]() .
.
It is also known that the centroid of ![]() is a third of the way between vertex
is a third of the way between vertex ![]() and
and ![]() , the vertex farthest from the plane. Since
, the vertex farthest from the plane. Since ![]() is a diagonal of the cube,
is a diagonal of the cube, ![]() . So the distance from the
. So the distance from the ![]() to
to ![]() is
is ![]() . So, the
. So, the ![]() from
from ![]() to the centroid is
to the centroid is  .
.
Thus the distance from ![]() to the plane is
to the plane is ![]() , and
, and ![]() .
.
Solution 3
Video Solution
https://youtube.com/watch?v=Wi-aqv8Ron0
See also
| 2011 AIME I (Problems • Answer Key • Resources) | ||
| Preceded by Problem 12 |
Followed by Problem 14 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.