Difference between revisions of "2011 AMC 10B Problems/Problem 25"
(→Solution) |
(→See Also) |
||
| Line 56: | Line 56: | ||
==See Also== | ==See Also== | ||
| + | == See Also == | ||
| + | |||
{{AMC10 box|year=2011|ab=B|num-b=24|after=Last Problem}} | {{AMC10 box|year=2011|ab=B|num-b=24|after=Last Problem}} | ||
Revision as of 20:03, 18 February 2013
Contents
Problem
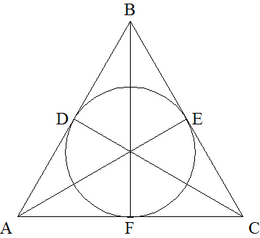
Let ![]() be a triangle with sides
be a triangle with sides ![]() and
and ![]() . For
. For ![]() , if
, if ![]() and
and ![]() and
and ![]() are the points of tangency of the incircle of
are the points of tangency of the incircle of ![]() to the sides
to the sides ![]() and
and ![]() respectively, then
respectively, then ![]() is a triangle with side lengths
is a triangle with side lengths ![]() and
and ![]() if it exists. What is the perimeter of the last triangle in the sequence
if it exists. What is the perimeter of the last triangle in the sequence ![]() ?
?
![]()
Solution
By constructing the bisectors of each angle and the perpendicular radii of the incircle the triangle consists of 3 kites.
Hence ![]() and
and ![]() and
and ![]() . Let
. Let ![]() and
and ![]() gives three equations:
gives three equations:
![]()
![]()
![]()
(where ![]() for the first triangle.)
for the first triangle.)
Solving gives:
![]()
![]()
![]()
Subbing in gives that ![]() has sides of
has sides of ![]() .
.
![]() can easily be derivied from this as the sides still differ by 1 hence the above solutions still work (now with
can easily be derivied from this as the sides still differ by 1 hence the above solutions still work (now with ![]() ). All additional triangles will differ by one as the solutions above differ by one so this process can be repeated indefinately until the side lengths no longer form a triangle.
). All additional triangles will differ by one as the solutions above differ by one so this process can be repeated indefinately until the side lengths no longer form a triangle.
Subbing in gives ![]() with sides
with sides ![]() .
.
![]() has sides
has sides ![]() .
.
![]() has sides
has sides ![]() .
.
![]() has sides
has sides ![]() .
.
![]() has sides
has sides ![]() .
.
![]() has sides
has sides ![]() .
.
![]() has sides
has sides ![]() .
.
![]() has sides
has sides ![]() .
.
![]() would have sides
would have sides ![]() but these length do not make a
triangle as
but these length do not make a
triangle as ![]() .
.
Hence the perimeter is ![]()
![]()
See Also
See Also
| 2011 AMC 10B (Problems • Answer Key • Resources) | ||
| Preceded by Problem 24 |
Followed by Last Problem | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||