Difference between revisions of "2017 AMC 12A Problems/Problem 22"
(→Solution: changed percentages to fractions) |
Isabelchen (talk | contribs) m (→Remark) |
||
| (11 intermediate revisions by 7 users not shown) | |||
| Line 2: | Line 2: | ||
A square is drawn in the Cartesian coordinate plane with vertices at <math>(2, 2)</math>, <math>(-2, 2)</math>, <math>(-2, -2)</math>, <math>(2, -2)</math>. A particle starts at <math>(0,0)</math>. Every second it moves with equal probability to one of the eight lattice points (points with integer coordinates) closest to its current position, independently of its previous moves. In other words, the probability is <math>1/8</math> that the particle will move from <math>(x, y)</math> to each of <math>(x, y + 1)</math>, <math>(x + 1, y + 1)</math>, <math>(x + 1, y)</math>, <math>(x + 1, y - 1)</math>, <math>(x, y - 1)</math>, <math>(x - 1, y - 1)</math>, <math>(x - 1, y)</math>, or <math>(x - 1, y + 1)</math>. The particle will eventually hit the square for the first time, either at one of the 4 corners of the square or at one of the 12 lattice points in the interior of one of the sides of the square. The probability that it will hit at a corner rather than at an interior point of a side is <math>m/n</math>, where <math>m</math> and <math>n</math> are relatively prime positive integers. What is <math>m + n</math>? | A square is drawn in the Cartesian coordinate plane with vertices at <math>(2, 2)</math>, <math>(-2, 2)</math>, <math>(-2, -2)</math>, <math>(2, -2)</math>. A particle starts at <math>(0,0)</math>. Every second it moves with equal probability to one of the eight lattice points (points with integer coordinates) closest to its current position, independently of its previous moves. In other words, the probability is <math>1/8</math> that the particle will move from <math>(x, y)</math> to each of <math>(x, y + 1)</math>, <math>(x + 1, y + 1)</math>, <math>(x + 1, y)</math>, <math>(x + 1, y - 1)</math>, <math>(x, y - 1)</math>, <math>(x - 1, y - 1)</math>, <math>(x - 1, y)</math>, or <math>(x - 1, y + 1)</math>. The particle will eventually hit the square for the first time, either at one of the 4 corners of the square or at one of the 12 lattice points in the interior of one of the sides of the square. The probability that it will hit at a corner rather than at an interior point of a side is <math>m/n</math>, where <math>m</math> and <math>n</math> are relatively prime positive integers. What is <math>m + n</math>? | ||
| + | |||
| + | <math> \textbf{(A) } 4 \qquad\textbf{(B) } 5 \qquad\textbf{(C) } 7 \qquad\textbf{(D) } 15 \qquad\textbf{(E) } 39 </math> | ||
==Solution== | ==Solution== | ||
| Line 13: | Line 15: | ||
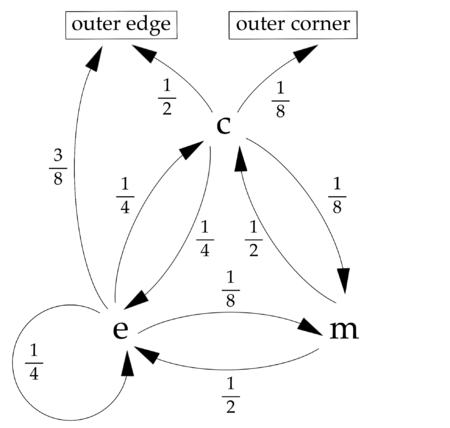
Starting at an inside edge, there is a <math>\frac{2}{8}</math> chance of moving to another inside edge, a <math>\frac{2}{8}</math> chance of moving to an inside corner, a <math>\frac{1}{8}</math> chance of moving into the middle, and a <math>\frac{3}{8}</math> chance of reaching an outside edge and stopping. Therefore, | Starting at an inside edge, there is a <math>\frac{2}{8}</math> chance of moving to another inside edge, a <math>\frac{2}{8}</math> chance of moving to an inside corner, a <math>\frac{1}{8}</math> chance of moving into the middle, and a <math>\frac{3}{8}</math> chance of reaching an outside edge and stopping. Therefore, | ||
| − | <cmath>e = \frac{1}{4}e + \frac{1}{4}c + \frac{1}{8}m + \frac{3}{8} | + | <cmath>e = \frac{1}{4}e + \frac{1}{4}c + \frac{1}{8}m + \frac{3}{8}\cdot 0 = \frac{1}{4}e + \frac{1}{4}c + \frac{1}{8}m.</cmath> |
Starting at an inside corner, there is a <math>\frac{2}{8}</math> chance of moving to an inside edge, a <math>\frac{1}{8}</math> chance of moving into the middle, a <math>\frac{4}{8}</math> chance of moving to an outside edge and stopping, and finally a <math>\frac{1}{8}</math> chance of reaching that elusive outside corner. This gives | Starting at an inside corner, there is a <math>\frac{2}{8}</math> chance of moving to an inside edge, a <math>\frac{1}{8}</math> chance of moving into the middle, a <math>\frac{4}{8}</math> chance of moving to an outside edge and stopping, and finally a <math>\frac{1}{8}</math> chance of reaching that elusive outside corner. This gives | ||
| − | <cmath>c = \frac{1}{4}e + \frac{1}{8}m + \frac{1}{2}0 + \frac{1}{8} | + | <cmath>c = \frac{1}{4}e + \frac{1}{8}m + \frac{1}{2}0 + \frac{1}{8}\cdot 1 = \frac{1}{4}e + \frac{1}{8}m + \frac{1}{8}.</cmath> |
Solving this system of equations gives | Solving this system of equations gives | ||
| Line 27: | Line 29: | ||
Since the particle starts at <math>(0, 0),</math> it is <math>m</math> we are looking for, so the final answer is | Since the particle starts at <math>(0, 0),</math> it is <math>m</math> we are looking for, so the final answer is | ||
| − | <cmath>4 + 35 = \textbf{(E) }39.</cmath> | + | <cmath>4 + 35 = \boxed{\textbf{(E) }39}.</cmath> |
| + | |||
| + | ==Remark (Markov Chain)== | ||
| + | |||
| + | [[File:2017AMC12AP22.png|center|450px]] | ||
| + | |||
| + | This problem can be modeled as an [https://en.wikipedia.org/wiki/Absorbing_Markov_chain Absorbing Markov Chain]. | ||
| + | |||
| + | [https://artofproblemsolving.com/wiki/index.php/2014_AMC_12B_Problems/Problem_22 2014 AMC12B Problem 22] is a similar problem that can be solved by using an Absorbing Markov Chain. | ||
| + | |||
| + | ~[https://artofproblemsolving.com/wiki/index.php/User:Isabelchen isabelchen] | ||
| + | |||
| + | ==Video Solutions== | ||
| + | https://www.youtube.com/watch?v=rz-Ma_O2bT4 | ||
| + | |||
| + | Solution by Richard Rusczyk - | ||
| + | https://www.youtube.com/watch?v=ixDXFRffUZ4&list=PLyhPcpM8aMvLZmuDnM-0vrFniLpo7Orbp&index=2 | ||
| + | - AMBRIGGS | ||
==See Also== | ==See Also== | ||
{{AMC12 box|year=2017|ab=A|num-b=21|num-a=23}} | {{AMC12 box|year=2017|ab=A|num-b=21|num-a=23}} | ||
{{MAA Notice}} | {{MAA Notice}} | ||
Latest revision as of 10:41, 4 December 2023
Problem
A square is drawn in the Cartesian coordinate plane with vertices at ![]() ,
, ![]() ,
, ![]() ,
, ![]() . A particle starts at
. A particle starts at ![]() . Every second it moves with equal probability to one of the eight lattice points (points with integer coordinates) closest to its current position, independently of its previous moves. In other words, the probability is
. Every second it moves with equal probability to one of the eight lattice points (points with integer coordinates) closest to its current position, independently of its previous moves. In other words, the probability is ![]() that the particle will move from
that the particle will move from ![]() to each of
to each of ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , or
, or ![]() . The particle will eventually hit the square for the first time, either at one of the 4 corners of the square or at one of the 12 lattice points in the interior of one of the sides of the square. The probability that it will hit at a corner rather than at an interior point of a side is
. The particle will eventually hit the square for the first time, either at one of the 4 corners of the square or at one of the 12 lattice points in the interior of one of the sides of the square. The probability that it will hit at a corner rather than at an interior point of a side is ![]() , where
, where ![]() and
and ![]() are relatively prime positive integers. What is
are relatively prime positive integers. What is ![]() ?
?
![]()
Solution
We let ![]() and
and ![]() be the probability of reaching a corner before an edge when starting at an "inside corner" (e.g.
be the probability of reaching a corner before an edge when starting at an "inside corner" (e.g. ![]() ), an "inside edge" (e.g.
), an "inside edge" (e.g. ![]() ), and the middle respectively.
), and the middle respectively.
Starting in the middle, there is a ![]() chance of moving to an inside edge and a
chance of moving to an inside edge and a ![]() chance of moving to an inside corner, so
chance of moving to an inside corner, so
![]()
Starting at an inside edge, there is a ![]() chance of moving to another inside edge, a
chance of moving to another inside edge, a ![]() chance of moving to an inside corner, a
chance of moving to an inside corner, a ![]() chance of moving into the middle, and a
chance of moving into the middle, and a ![]() chance of reaching an outside edge and stopping. Therefore,
chance of reaching an outside edge and stopping. Therefore,
![]()
Starting at an inside corner, there is a ![]() chance of moving to an inside edge, a
chance of moving to an inside edge, a ![]() chance of moving into the middle, a
chance of moving into the middle, a ![]() chance of moving to an outside edge and stopping, and finally a
chance of moving to an outside edge and stopping, and finally a ![]() chance of reaching that elusive outside corner. This gives
chance of reaching that elusive outside corner. This gives
![]()
Solving this system of equations gives
![]()
![]()
![]()
Since the particle starts at ![]() it is
it is ![]() we are looking for, so the final answer is
we are looking for, so the final answer is
![]()
Remark (Markov Chain)
This problem can be modeled as an Absorbing Markov Chain.
2014 AMC12B Problem 22 is a similar problem that can be solved by using an Absorbing Markov Chain.
Video Solutions
https://www.youtube.com/watch?v=rz-Ma_O2bT4
Solution by Richard Rusczyk - https://www.youtube.com/watch?v=ixDXFRffUZ4&list=PLyhPcpM8aMvLZmuDnM-0vrFniLpo7Orbp&index=2 - AMBRIGGS
See Also
| 2017 AMC 12A (Problems • Answer Key • Resources) | |
| Preceded by Problem 21 |
Followed by Problem 23 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.