2023 AIME I Problems/Problem 12
Contents
Problem
Let ![]() be an equilateral triangle with side length
be an equilateral triangle with side length ![]() Points
Points ![]()
![]() and
and ![]() lie on
lie on ![]()
![]() and
and ![]() respectively, with
respectively, with ![]()
![]() and
and ![]() Point
Point ![]() inside
inside ![]() has the property that
has the property that ![]() Find
Find ![]()
Diagram
![[asy] /* Made by MRENTHUSIASM */ size(300); pair A, B, C, D, E, F, P; A = 55*sqrt(3)/3 * dir(90); B = 55*sqrt(3)/3 * dir(210); C = 55*sqrt(3)/3 * dir(330); D = B + 7*dir(0); E = A + 25*dir(C-A); F = A + 40*dir(B-A); P = intersectionpoints(Circle(D,54*sqrt(19)/19),Circle(F,5*sqrt(19)/19))[0]; draw(anglemark(A,E,P,20),red); draw(anglemark(B,F,P,20),red); draw(anglemark(C,D,P,20),red); add(pathticks(anglemark(A,E,P,20), n = 1, r = 0.2, s = 12, red)); add(pathticks(anglemark(B,F,P,20), n = 1, r = 0.2, s = 12, red)); add(pathticks(anglemark(C,D,P,20), n = 1, r = 0.2, s = 12, red)); draw(A--B--C--cycle^^P--E^^P--F^^P--D); dot("$A$",A,1.5*dir(A),linewidth(4)); dot("$B$",B,1.5*dir(B),linewidth(4)); dot("$C$",C,1.5*dir(C),linewidth(4)); dot("$D$",D,1.5*S,linewidth(4)); dot("$E$",E,1.5*dir(30),linewidth(4)); dot("$F$",F,1.5*dir(150),linewidth(4)); dot("$P$",P,1.5*dir(-30),linewidth(4)); label("$7$",midpoint(B--D),1.5*S,red); label("$30$",midpoint(C--E),1.5*dir(30),red); label("$40$",midpoint(A--F),1.5*dir(150),red); [/asy]](http://latex.artofproblemsolving.com/f/3/b/f3b6ad1973c53a1977ced1415536613f6c1bf609.png) ~MRENTHUSIASM
~MRENTHUSIASM
Solution 1 (Coordinates Bash)
By Miquel's theorem, ![]() (intersection of circles)
(intersection of circles)![]() . The law of cosines can be used to compute
. The law of cosines can be used to compute ![]() ,
, ![]() , and
, and ![]() . Toss the points on the coordinate plane; let
. Toss the points on the coordinate plane; let ![]() ,
, ![]() , and
, and ![]() , where we will find
, where we will find ![]() with
with ![]() .
.
By the extended law of sines, the radius of circle ![]() is
is ![]() . Its center lies on the line
. Its center lies on the line ![]() , and the origin is a point on it, so
, and the origin is a point on it, so ![]() .
.
The radius of circle ![]() is
is ![]() . The origin is also a point on it, and its center is on the line
. The origin is also a point on it, and its center is on the line ![]() , so
, so ![]() .
.
The equations of the two circles are  These equations simplify to
These equations simplify to  Subtracting these two equations gives that both their points of intersection,
Subtracting these two equations gives that both their points of intersection, ![]() and
and ![]() , lie on the line
, lie on the line ![]() . Hence,
. Hence,  . To scale, the configuration looks like the figure below:
. To scale, the configuration looks like the figure below:
![[asy] /* Made by MRENTHUSIASM */ size(400); pair A, B, C, D, E, F, P; A = 55*sqrt(3)/3 * dir(90); B = 55*sqrt(3)/3 * dir(210); C = 55*sqrt(3)/3 * dir(330); D = B + 7*dir(0); E = A + 25*dir(C-A); F = A + 40*dir(B-A); P = intersectionpoints(Circle(D,54*sqrt(19)/19),Circle(F,5*sqrt(19)/19))[0]; filldraw(D--E--F--cycle,yellow); draw(A--B--C--cycle); draw(circumcircle(A,E,F)^^circumcircle(B,D,F)^^circumcircle(C,D,E),blue); dot("$A$",A,1.5*dir(A),linewidth(4)); dot("$B$",B,1.5*dir(B),linewidth(4)); dot("$C$",C,1.5*dir(C),linewidth(4)); dot("$D$",D,1.5*S,linewidth(4)); dot("$E$",E,1.5*dir(30),linewidth(4)); dot("$F$",F,1.5*dir(150),linewidth(4)); dot("$P$",P,1.5*dir(-30),linewidth(4)); label("$7$",midpoint(B--D),1.5*S,red); label("$30$",midpoint(C--E),1.5*dir(30),red); label("$40$",midpoint(A--F),1.5*dir(150),red); [/asy]](http://latex.artofproblemsolving.com/2/9/2/292e73b53e11391e163abe09cf15ae80b454bb6a.png)
![]() Basic angle chasing gives
Basic angle chasing gives ![]() Because
Because ![]() which means that
which means that ![]() is cyclic, and that
is cyclic, and that ![]() passes through the circumcircle of triangle
passes through the circumcircle of triangle ![]() Similar reasoning leads us to the fact that
Similar reasoning leads us to the fact that ![]() also passes through the circumcircles of triangles
also passes through the circumcircles of triangles ![]() and
and ![]() which means that
which means that ![]() Continue as above.
Continue as above.
Solution 2 (Vectors/Complex)
Denote ![]() .
.
In ![]() , we have
, we have ![]() .
Thus,
.
Thus,
![]()
Taking the real and imaginary parts, we get
![]()
In ![]() , analogous to the analysis of
, analogous to the analysis of ![]() above, we get
above, we get
![]()
Taking ![]() , we get
, we get
![]()
Taking ![]() , we get
, we get
![]()
Taking ![]() , we get
, we get
![]()
Therefore,

Therefore, ![]() .
.
~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)
Solution 3 (Synthetic)
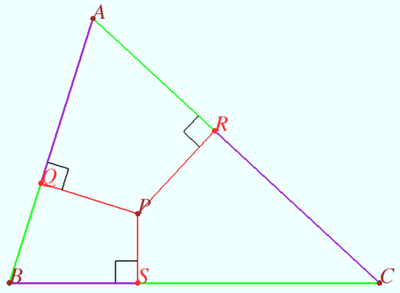
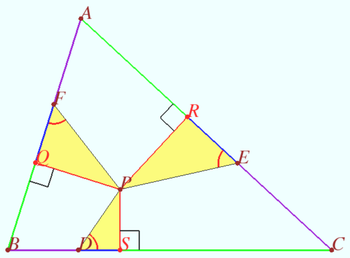
Drop the perpendiculars from ![]() to
to ![]() ,
, ![]() ,
, ![]() , and call them
, and call them ![]() and
and ![]() respectively. This gives us three similar right triangles
respectively. This gives us three similar right triangles ![]() ,
, ![]() , and
, and ![]()
The sum of the perpendiculars to a point ![]() within an equilateral triangle is always constant, so we have that
within an equilateral triangle is always constant, so we have that ![]()
The sum of the lengths of the alternating segments split by the perpendiculars from a point ![]() within an equilateral triangle is always equal to half the perimeter, so
within an equilateral triangle is always equal to half the perimeter, so ![]() which means that
which means that ![]()
Finally, ![]()
Thus, ![]()
~anon
Claim
a) Carnot's theorem. Given triangle ![]() and point
and point ![]() Let
Let ![]()
![]()
![]() doesn't have to be inside
doesn't have to be inside ![]()
Prove that ![]()
b) Let ![]() be the equilateral triangle. Prove that
be the equilateral triangle. Prove that ![]() (The sum of the lengths of the alternating segments split by the perpendiculars from a point
(The sum of the lengths of the alternating segments split by the perpendiculars from a point ![]() within an equilateral triangle is equal to half the perimeter.)
within an equilateral triangle is equal to half the perimeter.)
Proof
a) ![]()
![]()
![]()
![]()
![]() b)
b) ![]()
![]()
![]()
![]()
![]()
![]()
vladimir.shelomovskii@gmail.com, vvsss
Solution 4 (Law of Cosines)
This solution is inspired by AIME 1999 Problem 14 Solution 2 (a similar question)
Draw line segments from ![]() to points
to points ![]() ,
, ![]() , and
, and ![]() . And label the angle measure of
. And label the angle measure of ![]() ,
, ![]() , and
, and ![]() to be
to be ![]()
Using Law of Cosines (note that ![]() )
)

We can perform this operation ![]() :
:
Leaving us with (after combining and simplifying)
![]()
Therefore, we want to solve for ![]()
Notice that ![]()
We can use Law of Cosines again to solve for the sides of ![]() , which have side lengths of
, which have side lengths of ![]() ,
, ![]() , and
, and ![]() , and area
, and area ![]() .
.
Label the lengths of ![]() ,
, ![]() , and
, and ![]() to be
to be ![]() ,
, ![]() , and
, and ![]() .
.
Therefore, using the ![]() area formula,
area formula,
![\begin{align*} [\triangle{DEF}] &= \frac{1}{2}\cdot\sin{120°}\cdot(xy+yz+zx) = 120\sqrt{3} \\ xy+yz+zx &= 2^5\cdot3\cdot5 \end{align*}](http://latex.artofproblemsolving.com/b/0/1/b013670446f0ebbd1bf3892a8d8c9144014c1d76.png)
In addition, we know that

By using Law of Cosines for ![]() ,
, ![]() , and
, and ![]() respectively
respectively
Because we want ![]() , which is
, which is ![]() , we see that
, we see that

So plugging the results back into the equation before, we get

Giving us ![]()
Solution 5 (Combining Solutions 3 and 4)
We begin by using the fact stated in Solution 3 that, for any point in an equilateral triangle, the lengths of the three perpendicular lines dropped to the sides of the triangle add up to the altitude of that triangle. To make things simple, let's assign ![]() . We can label these three perpendiculars as:
. We can label these three perpendiculars as:
![]() Simplifying, we get
Simplifying, we get
![]() Now, as stated and quoting Solution 4,
"Draw line segments from
Now, as stated and quoting Solution 4,
"Draw line segments from ![]() to points
to points ![]() ,
, ![]() , and
, and ![]() . [We know that] the angle measure of
. [We know that] the angle measure of ![]() ,
, ![]() , and
, and ![]() is
is ![]()
Using Law of Cosines (note that ![]() )
)

We can perform this operation ![]() :
:
Leaving us with (after combining and simplifying)
![]() ".
".
Now, we can use our previous equation along with this one to get:
![]() .
.
This equation becomes:
![]() As so, our answer is
As so, our answer is
![]() ~Solution by armang32324 (Mathemagics Club)
~Solution by armang32324 (Mathemagics Club)
Solution 6
By the law of cosines,
![]() Similarly we get
Similarly we get ![]() and
and ![]() .
. ![]() implies that
implies that ![]() ,
, ![]() , and
, and ![]() are three cyclic quadrilaterals, as shown below:
are three cyclic quadrilaterals, as shown below:
![[asy] /* Made by MRENTHUSIASM */ size(400); pair A, B, C, D, E, F, P; A = 55*sqrt(3)/3 * dir(90); B = 55*sqrt(3)/3 * dir(210); C = 55*sqrt(3)/3 * dir(330); D = B + 7*dir(0); E = A + 25*dir(C-A); F = A + 40*dir(B-A); P = intersectionpoints(Circle(D,54*sqrt(19)/19),Circle(F,5*sqrt(19)/19))[0]; draw(anglemark(A,E,P,20),red); draw(anglemark(B,F,P,20),red); draw(anglemark(C,D,P,20),red); add(pathticks(anglemark(A,E,P,20), n = 1, r = 0.2, s = 12, red)); add(pathticks(anglemark(B,F,P,20), n = 1, r = 0.2, s = 12, red)); add(pathticks(anglemark(C,D,P,20), n = 1, r = 0.2, s = 12, red)); draw(A--B--C--cycle^^P--E^^P--F^^P--D); draw(P--A^^P--B^^P--C,dashed); draw(circumcircle(A,E,F)^^circumcircle(B,D,F)^^circumcircle(C,D,E),blue); dot("$A$",A,1.5*dir(A),linewidth(4)); dot("$B$",B,1.5*dir(B),linewidth(4)); dot("$C$",C,1.5*dir(C),linewidth(4)); dot("$D$",D,1.5*S,linewidth(4)); dot("$E$",E,1.5*dir(30),linewidth(4)); dot("$F$",F,1.5*dir(150),linewidth(4)); dot("$P$",P,1.5*dir(-30),linewidth(4)); label("$7$",midpoint(B--D),1.5*S,red); label("$30$",midpoint(C--E),1.5*dir(30),red); label("$40$",midpoint(A--F),1.5*dir(150),red); [/asy]](http://latex.artofproblemsolving.com/c/a/4/ca4c97bb05b26f81123a4a27e8cf1e5b3c7b0732.png) Using the law of sines in each,
Using the law of sines in each,
![]() So we can set
So we can set ![]() ,
, ![]() , and
, and ![]() . Let
. Let ![]() ,
, ![]() , and
, and ![]() . Applying Ptolemy theorem in the cyclic quadrilaterals,
. Applying Ptolemy theorem in the cyclic quadrilaterals,
![\[\begin{cases}AP\cdot FE=AF\cdot PE+AE\cdot PF,\\CP\cdot ED=CE\cdot PD+CD\cdot PE,\\BP\cdot DF=BD\cdot PF+BF\cdot PD.\end{cases} \implies \begin{cases} 1225k=40e+25f,\\1764k=30d+48e,\\169k=15d+7f, \end{cases}\]](http://latex.artofproblemsolving.com/2/9/7/297912a1434ac5ec975494ce5b2033976ff72466.png) We can solve out
We can solve out ![]() ,
, ![]() ,
, ![]() . By the law of cosines in
. By the law of cosines in ![]() ,
,  . The law of sines yield
. The law of sines yield ![]() .
Lastly,
.
Lastly, ![]() , then
, then ![]() . The answer is
. The answer is
![]()
Video Solution
https://www.youtube.com/watch?v=EdwM8GpY_yc
~MathProblemSolvingSkills.com
Animated Video Solution
~Star League (https://starleague.us)
Video Solution by MOP 2024
See also
| 2023 AIME I (Problems • Answer Key • Resources) | ||
| Preceded by Problem 11 |
Followed by Problem 13 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.