Difference between revisions of "2023 AMC 12A Problems/Problem 20"

Revision as of 23:30, 10 November 2023

Problem

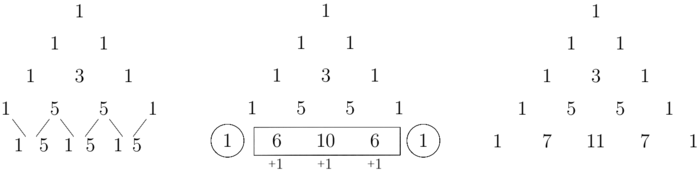
Rows 1, 2, 3, 4, and 5 of a triangular array of integers are shown below.

$[asy] size(4.5cm); label("$1$", (0,0)); label("$1$", (-0.5,-2/3)); label("$1$", (0.5,-2/3)); label("$1$", (-1,-4/3)); label("$3$", (0,-4/3)); label("$1$", (1,-4/3)); label("$1$", (-1.5,-2)); label("$5$", (-0.5,-2)); label("$5$", (0.5,-2)); label("$1$", (1.5,-2)); label("$1$", (-2,-8/3)); label("$7$", (-1,-8/3)); label("$11$", (0,-8/3)); label("$7$", (1,-8/3)); label("$1$", (2,-8/3)); [/asy]$

Each row after the first row is formed by placing a 1 at each end of the row, and each interior entry is 1 greater than the sum of the two numbers diagonally above it in the previous row. What is the units digits of the sum of the 2023 numbers in the 2023rd row?

$\textbf{(A) } 1 \qquad \textbf{(B) } 3 \qquad \textbf{(C) } 5 \qquad \textbf{(D) } 7 \qquad \textbf{(E) } 9$

Solution 1

First, let $R(n)$ be the sum of the $n$ th row. Now, with some observations and math instinct, we can guess that $R(n) = 2^n - n$ .

Now we try to prove it by induction,

$R(1) = 2^n - n = 2^1 - 1 = 1$ (works for base case)

$R(k) = 2^k - k$

$R(k+1) = 2^{k+1} - (k + 1) = 2(2^k) - k - 1$

By definition from the question, the next row is always $:$

Double the sum of last row (Imagine ach number from last row branches off toward left and right to the next row), plus # of new row, minus 2 (leftmost and rightmost are just 1)

Which gives us $:$

$2(2^k - k) + (k + 1) - 2 = 2(2^k) - k - 1$

Hence, proven

Last, simply substitute $n = 2023$ , we get $R(2023) = 2^{2023} - 2023$

Last digit of $2^{2023}$ is $8$ , $8-3 = \boxed{\textbf{(C) } 5}$

~lptoggled

Solution 2

Let the sum of the numbers in row $2022$ be $S_{2022}$ . Let each number in row $2022$ be $x_i$ where $1 \leq i \leq 2022$ .

Then $\begin{align*} S_{2023}&=1+(x_1+x_2+1)+(x_2+x_3+1)+...+(x_{2021}+x_{2022}+ 1)+1 \\ S_{2023}&=x_1+2(S_{2022}-x_1-x_{2022})+2023+x_{2022} \\ S_{2023} &= 2S_{2022} + 2021 \end{align*}$ From this we can establish: $\begin{align*} S_n &= 2S_{n-1} + n-2 \\ S_{n-1} &= 2S_{n-2} + n-3 \\ S_n - S_{n-1} &= 2S_{n-1} - 2S_{n-2} + 1 \end{align*}$

Let $B_{n} = S_n - S_{n-1}$

From this we have: $\begin{align*} B_n + 1 &= 2(B_{n-1} + 1) \\ B_n &= 2^{n-1} - 1 \\ S_n - S_{n-1} &= 2^{n-1} - 1 \\ S_n &= 2^{n-1} + 2^{n-2} + ... + 2^1 - (n-1) + S_1 \\ S_n &= 2^n - n \\ S_{2023} &= 2^{2023} - 2023 \end{align*}$

The problem requires us to find the last digit of $S_{2023}$ . We can use modular arithmetic. $\begin{align*} S_{2023} &= 2^{2023} - 2023 \\ 2^{2023} - 2023 &\equiv 8 - 3\pmod{10} \\ &\equiv \boxed{\textbf{(C) } 5} \pmod{10} \\ \end{align*}$ ~luckuso

Solution 3 (Recursion)

Let the sum of the $n^{th}$ row be $S_n$ .

For each of the $n-2$ non-1 entries in the $n^{th}$ row, they are equal to the sum of the $2$ numbers diagonally above it in the $n-1^{th}$ row plus $1$ . Therefore all $n-3$ non-1 entries in the $n-1^{th}$ row appear twice in sum for the $n-2$ non-1 entries in the $n^{th}$ row, the two $1$ s on each end of the $n-1^{th}$ row only appear once in the sum for the $n-2$ non-1 entries in the $n^{th}$ row. Additionally, additional $1$ s are placed at each end of the $n^{th}$ row. Hence, $S_n = 2(S_{n-1} - 1) + n-2 + 1 + 1 = 2 S_{n-1} + n - 2$

$S_n = 2 S_{n-1} + n - 2$

$S_4 = 1+5+5+1 = 12$ , $S_5 = 1+7+11+7+1 = 27$ . By using the recursive formula, $S_5 = 2 \cdot S_4 + 5-2 = 27$

$S_n = 2 S_{n-1} + n - 2$ $S_n + n = 2 S_{n-1} + 2n - 2$ $S_n + n = 2( S_{n-1} + n - 1)$ $S_n + n$ is a geometric sequence by a ratio of $2$

$\because \quad S_1 = 1$

$\therefore \quad S_n + n = 2^n$ , $S_n = 2^n - n$

$S_{2023} = 2^{2023} - 2023$

The unit digit of powers of $2$ is periodic by a cycle of $4$ digits: $2$ , $4$ , $8$ , $6$ . $2023 = 3 \mod 4$ , the unit digit of $2^{2023}$ is $8$ .

Therefore, the unit digit of $S_{2023}$ is $8-3 = \boxed{\textbf{(C) } 5}$

~isabelchen

Video Solution 1 by OmegaLearn

https://youtu.be/MnR5VXAXDeU

Video Solution

https://youtu.be/EVHnJFOW4Ys

~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)

@@ Line 95: / Line 95: @@
 Let the sum of the <math>n^{th}</math> row be <math>S_n</math>.
-For each of the <math>n-2</math> non-1 entries in the <math>n^{th}</math> row, they are equal to the sum of the <math>2</math> numbers diagonally above it in the <math>n-1^{th}</math> row plus <math>1</math>. Therefore all <math>n-3</math> non-1 entries in the <math>n-1^{th}</math> appear twice in sum for the <math>n-2</math> non-1 entries in the <math>n^{th}</math> row, the <math>2</math> <math>1</math>s on each end only appear once in the sum for the <math>n-2</math> non-1 entries in the <math>n^{th}</math> row. Additionally, additional <math>1</math>s are placed at each end of the row. Hence, <math>S_n = 2(S_{n-1} - 1) + n-2 + 1 + 1 = 2 S_{n-1} + n - 2</math>
+For each of the <math>n-2</math> non-1 entries in the <math>n^{th}</math> row, they are equal to the sum of the <math>2</math> numbers diagonally above it in the <math>n-1^{th}</math> row plus <math>1</math>. Therefore all <math>n-3</math> non-1 entries in the <math>n-1^{th}</math> row appear twice in sum for the <math>n-2</math> non-1 entries in the <math>n^{th}</math> row, the two <math>1</math>s on each end of the <math>n-1^{th}</math> row only appear once in the sum for the <math>n-2</math> non-1 entries in the <math>n^{th}</math> row. Additionally, additional <math>1</math>s are placed at each end of the <math>n^{th}</math> row. Hence, <math>S_n = 2(S_{n-1} - 1) + n-2 + 1 + 1 = 2 S_{n-1} + n - 2</math>
 <cmath>S_n = 2 S_{n-1} + n - 2</cmath>

2023 AMC 12A (Problems • Answer Key • Resources)
Preceded by Problem 19	Followed by Problem 21
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions

Page

Toolbox

Search