2023 AMC 12A Problems/Problem 21
- The following problem is from both the 2023 AMC 10A #25 and 2023 AMC 12A #21, so both problems redirect to this page.
Contents
[hide]- 1 Problem
- 2 Diagram
- 3 Solution 1
- 4 Solution 2 (Cheese + Actual way)
- 5 Solution 3
- 6 Solution 4
- 7 Solution 5
- 8 Solution 6 (Case Work(similar to 3))
- 9 Solution 7 (efficient)
- 10 Solution 8 (Dodecahedron Schlegel (Planar Graph) Diagram)
- 11 Solution 9 (Symmetry)
- 12 Video Solution by Little Fermat
- 13 Video Solution by Math-X
- 14 Video Solution
- 15 Video Solution by OmegaLearn
- 16 Video solution by MegaMath
- 17 Video Solution by epicbird08
- 18 Vide Solution by SpreadTheMathLove(Casework and Complementary)
- 19 Video Solution
- 20 Video Solution by TheBeautyofMath
- 21 See also
Problem
If ![]() and
and ![]() are vertices of a polyhedron, define the distance
are vertices of a polyhedron, define the distance ![]() to be the minimum number of edges of the polyhedron one must traverse in order to connect
to be the minimum number of edges of the polyhedron one must traverse in order to connect ![]() and
and ![]() . For example, if
. For example, if ![]() is an edge of the polyhedron, then
is an edge of the polyhedron, then ![]() , but if
, but if ![]() and
and ![]() are edges and
are edges and ![]() is not an edge, then
is not an edge, then ![]() . Let
. Let ![]() ,
, ![]() , and
, and ![]() be randomly chosen distinct vertices of a regular icosahedron (regular polyhedron made up of 20 equilateral triangles). What is the probability that
be randomly chosen distinct vertices of a regular icosahedron (regular polyhedron made up of 20 equilateral triangles). What is the probability that ![]() ?
?
![]()
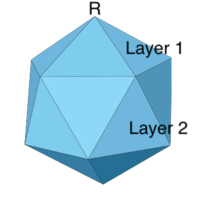
Diagram
Solution 1
To find the total amount of vertices we first find the amount of edges, and that is ![]() . Next, to find the amount of vertices we can use Euler's characteristic,
. Next, to find the amount of vertices we can use Euler's characteristic, ![]() , and therefore the amount of vertices is
, and therefore the amount of vertices is ![]()
So there are ![]() ways to choose 3 distinct points.
ways to choose 3 distinct points.
Now, the furthest distance we can get from one point to another point in an icosahedron is 3. Which gives us a range of ![]()
With some case work, we get two cases:
Case 1: ![]()
Since we have only one way to choose Q, that is, the opposite point from R, we have one option for Q and any of the other points could work for S.
Then, we get ![]() (ways to choose R × ways to choose Q × ways to choose S)
(ways to choose R × ways to choose Q × ways to choose S)
Case 2: ![]()
We can visualize the icosahedron as 4 rows, first row with 1 vertex, second row with 5 vertices, third row with 5 vertices and fourth row with 1 vertex. We set R as the one vertex on the first row, and we have 12 options for R. Then, Q can be any of the 5 points on the third row and finally S can be one of the 5 points on the second row.
Therefore, we have ![]() (ways to choose R × ways to choose Q × ways to choose S)
(ways to choose R × ways to choose Q × ways to choose S)
Hence, ![]()
~lptoggled, edited by ESAOPS and trevian1
Solution 2 (Cheese + Actual way)
In total, there are  ways to select the points. However, if we look at the denominators of
ways to select the points. However, if we look at the denominators of ![]() , they are
, they are ![]() which are not divisors of
which are not divisors of ![]() . Also
. Also ![]() is impossible as cases like
is impossible as cases like ![]() exist. The only answer choice left is
exist. The only answer choice left is ![]()
Note: this cheese is actually wrong because the total number of ways to select the points is actually ![]() as order matters, so all denominators are possible. Rather, you can arrive at the same conclusion by fixing R WLOG, leading to
as order matters, so all denominators are possible. Rather, you can arrive at the same conclusion by fixing R WLOG, leading to ![]() ways in total, which works for the original cheese. ~awesomeguy856
ways in total, which works for the original cheese. ~awesomeguy856
(Actual way)
Fix an arbitrary point, to select the rest ![]() points, there are
points, there are ![]() ways. To make
ways. To make ![]() . Which means there are in total
. Which means there are in total ![]() ways to make the distance the same.
ways to make the distance the same. ![]() ~bluesoul
~bluesoul
Solution 3
We can imagine the icosahedron as having 4 layers. 1 vertex at the top, 5 vertices below connected to the top vertex, 5 vertices below that which are 2 edges away from the top vertex, and one vertex at the bottom that is 3 edges away. WLOG because the icosahedron is symmetric around all vertices, we can say that R is the vertex at the top. So now, we just need to find the probability that S is on a layer closer to the top than Q. We can do casework on the layer S is on to get
![]() So the answer is
So the answer is ![]() .
.
-awesomeparrot
Solution 4
We can actually see that the probability that ![]() is the exact same as
is the exact same as ![]() because
because ![]() and
and ![]() have no difference. (In other words, we can just swap Q and S, meaning that can be called the same probability-wise.) Therefore, we want to find the probability that
have no difference. (In other words, we can just swap Q and S, meaning that can be called the same probability-wise.) Therefore, we want to find the probability that ![]() .
.
WLOG, we can rotate the icosahedron so that R is the top of the icosahedron. Then we can divide this into 2 cases:
1. They are on the second layer
There are 5 ways to put one point, and 4 ways to put the other point such that ![]() . So, there are
. So, there are ![]() ways to put them on the second layer.
ways to put them on the second layer.
2. They are on the third layer
There are 5 ways to put one point, and 4 ways to put the other point such that ![]() . So, there are
. So, there are ![]() ways to put them on the third layer.
ways to put them on the third layer.
The total number of ways to choose P and S are ![]() (because there are 12 vertices), so the probability that
(because there are 12 vertices), so the probability that ![]() is
is ![]() .
.
Therefore, the probability that ![]() is
is ![]()
~Ethanzhang1001
Solution 5
We know that there are ![]() faces. Each of those faces has
faces. Each of those faces has ![]() borders (since each is a triangle), and each edge is used as a border twice (for each face on either side). Thus, there are
borders (since each is a triangle), and each edge is used as a border twice (for each face on either side). Thus, there are ![]() edges.
edges.
Euler's formula states that ![]() for all convex polyhedra, so we know that
for all convex polyhedra, so we know that ![]() vertices.
vertices.
The answer can be counted by first counting the number of possible paths that will yield ![]() and dividing it by
and dividing it by ![]() (or
(or ![]() , depending on the approach). In either case, one will divide by
, depending on the approach). In either case, one will divide by ![]() somewhere in the denominator. We can then hope that there will be no factor of
somewhere in the denominator. We can then hope that there will be no factor of ![]() in the numerator (which would cancel the
in the numerator (which would cancel the ![]() in the denominator out), and answer the only option that has an
in the denominator out), and answer the only option that has an ![]() in the denominator:
in the denominator: ![]() .
.
~Technodoggo(minor edits by Gannit)
Additional note by "Fruitz": One can eliminate ![]() by symmetry if you swap the new sign.
by symmetry if you swap the new sign.
Another note by "andliu766": A shorter way to find the number of vertices and edges is to use the fact that the MAA logo is an icosahedron. :)
Solution 6 (Case Work(similar to 3))
WLOG, let R be at the top-most vertex of the icosahedron. There are ![]() cases where
cases where ![]() .
.
Case 1: ![]() is at the bottom-most vertex
is at the bottom-most vertex
If ![]() is at the bottom-most vertex, no matter where
is at the bottom-most vertex, no matter where ![]() is,
is, ![]() . The probability that
. The probability that ![]() is at the bottom-most vertex is
is at the bottom-most vertex is ![]()
Case 2: ![]() is at the second layer
is at the second layer
If ![]() is at the second layer,
is at the second layer, ![]() must be at the first layer, for
must be at the first layer, for ![]() to be true. The probability that
to be true. The probability that ![]() is at the second layer, and
is at the second layer, and ![]() is at the first layer is
is at the first layer is ![]()
![]()
Supplement
First, we have 20 faces of equilateral triangles. But each edge is shared by two faces hence there are thus ![]() edges.
edges.
Now by Euler's formula ![]()
Furthermore, the number of triangles (![]() ) that meet at one vertex can be found as follows. Note that there are
) that meet at one vertex can be found as follows. Note that there are ![]() total vertices. Without accounting for overcounting,
total vertices. Without accounting for overcounting, ![]() But since we now know that there are only
But since we now know that there are only ![]() vertices and that each vertex is shared by
vertices and that each vertex is shared by ![]() triangles, you find that there are 5 triangles that meet at one vertex.
triangles, you find that there are 5 triangles that meet at one vertex.
Once we pick R as the topmost vertex, there are 11 possible vertices remaining for ![]() Continue as follows in this solution.
Continue as follows in this solution.
~mathboy282
Solution 7 (efficient)
Since the icosahedron is symmetric polyhedron, we can rotate it so that R is on the topmost vertex. Since Q and
S basically the same, we can first count the probability that ![]() .
.
![]()
There are 5 points ![]() such that
such that ![]() . There is
. There is ![]() ways to choose Q and S in this case.
ways to choose Q and S in this case.
![]()
There are 5 points ![]() such that
such that ![]() . There is
. There is ![]() ways to choose Q and S in this case.
ways to choose Q and S in this case.
![]()
There is 1 point ![]() such that
such that ![]() . There is
. There is ![]() ways to choose Q and S in this case.
ways to choose Q and S in this case.
![]()
There are 11 points ![]() that are distinct from R. There is
that are distinct from R. There is ![]() ways to choose Q and S. There is
ways to choose Q and S. There is ![]() ways to choose Q and S such that
ways to choose Q and S such that ![]() . There is
. There is ![]() ways to choose Q and S such that
ways to choose Q and S such that ![]() . The probability that
. The probability that ![]() is therefore
is therefore ![]() which corresponds to answer choice
which corresponds to answer choice ![]()
~~afly
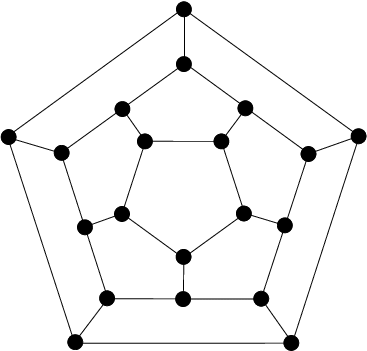
Solution 8 (Dodecahedron Schlegel (Planar Graph) Diagram)
Instead of thinking this problem as vertices of a icosahedron, think of it as faces of a dodecahedron. Our middle face is ![]() and we first choose
and we first choose ![]() and
and ![]() to be the faces with distance
to be the faces with distance ![]() from the middle face. There are
from the middle face. There are ![]() ways of doing that. Then we choose
ways of doing that. Then we choose ![]() and
and ![]() to be the faces with distance
to be the faces with distance ![]() from the middle face. There are
from the middle face. There are ![]() ways of doing that. Our answer is therefore
ways of doing that. Our answer is therefore 
~lopkiloinm
Note: You can do the same analysis on the vertices of the icosahedron using its diagram, which is less to draw because it has fewer (12) vertices and the same number (30) of edges. But this diagram is either less symmetrical or non-planar. (There's no good place to put the last vertex (diametrically opposite the first/central vertex), except in the same place as the first vertex.)
Solution 9 (Symmetry)
Note that the vertices of an icosahedron are in a ![]() configuration.
configuration.
We will denote the probability of event ![]() happening as
happening as ![]()
We should also note that ![]()
Also, ![]() since
since ![]() and
and ![]() are basically the same.
are basically the same.
Therefore, what we are trying to find is just ![]() which can easily be computed when we fix
which can easily be computed when we fix ![]() at the top vertex in the
at the top vertex in the ![]() structure.
structure.
Since all the points are distinct (stated in problem), the conditions are only satisfied where ![]() and
and ![]() are at
are at ![]() s of the
s of the ![]() structure.
structure.
![]() since we have to choose one of the
since we have to choose one of the ![]() out of
out of ![]() possible vertices and another one of
possible vertices and another one of ![]() out of
out of ![]() two times.
two times.
And the answer is ![]()
~jjaamm
Video Solution by Little Fermat
https://youtu.be/h2Pf2hvF1wE?si=5rhpccHQjb0-_X_Q&t=5615 ~little-fermat
Video Solution by Math-X
https://youtu.be/GP-DYudh5qU?si=khqcGMD9llQrHbKz&t=9770
~Math-X
Video Solution
https://youtu.be/4PSrAbrjKVg?si=G24hhBrhUPio9SZD
~MathProblemSolvingSkills.com
Video Solution by OmegaLearn
Video solution by MegaMath
https://www.youtube.com/watch?v=dxYw1wYHid4&t=12s
https://www.youtube.com/watch?v=1yLvQ0F5Z-E
Video Solution by epicbird08
~EpicBird08
Vide Solution by SpreadTheMathLove(Casework and Complementary)
https://www.youtube.com/watch?v=4FEwxwgbliQ
Video Solution
~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)
Video Solution by TheBeautyofMath
~IceMatrix
See also
| 2023 AMC 10A (Problems • Answer Key • Resources) | ||
| Preceded by Problem 24 |
Followed by Last Problem | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
| 2023 AMC 12A (Problems • Answer Key • Resources) | |
| Preceded by Problem 20 |
Followed by Problem 22 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()