2023 AMC 8 Problems/Problem 7

Problem

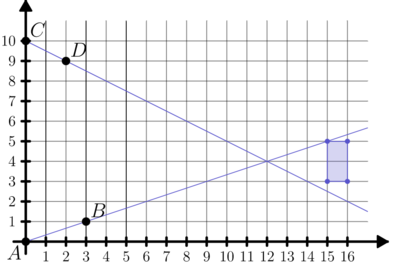
A rectangle, with sides parallel to the $x$ -axis and $y$ -axis, has opposite vertices located at $(15, 3)$ and $(16, 5)$ . A line drawn through points $A(0, 0)$ and $B(3, 1)$ . Another line is drawn through points $C(0, 10)$ and $D(2, 9)$ . How many points on the rectangle lie on at least one of the two lines?

$\textbf{(A)}\ 0 \qquad \textbf{(B)}\ 1 \qquad \textbf{(C)}\ 2 \qquad \textbf{(D)}\ 3 \qquad \textbf{(E)}\ 4$

Solution 1

If we extend the lines, we have

Hence, we see that the answer is $\boxed{\textbf{(B)}\ 1}$

~MrThinker

Solution 2

Note that the $y$ -intercept of line $AB$ and line $CD$ are $0$ and $10$ . If the analytic expression for line $AB$ is $y=k_{1}x$ , and the analytic expression for line $CD$ is $y=k_{2}x+10$ , we have equations: $3k_{1} = 1$ and $2k_{2} + 10 = 9$ . Solving these equations, we can find out that $k_{1} = \frac{1}{3}$ and $k_{2} = -\frac{1}{2}$ . Therefore, we can determine that the expression for line $AB$ is $y=\frac{1}{3}x$ . and the expression for line $CD$ is $y=-\frac{1}{2}x + 10$ . When $x=15$ , the coordinates that line $AB$ and line $CD$ pass through are $(15, 5)$ and $\left(15, \frac{5}{2}\right)$ , and $(15, 5)$ lies perfectly on one vertex of the rectangle while the $y$ coordinate of $\left(15, \frac{5}{2}\right)$ is out of the range $3 \leq y \leq 5$ (lower than the bottom left corner of the rectangle $(15, 3)$ ). Considering that the $y$ value of the line $CD$ will only decrease, and the $y$ value of the line $AB$ will only increase, there will not be another point on the rectangle that lies on either of the two lines. Thus, we can conclude that the answer is $\boxed{\textbf{(B)}\ 1}$

~\href{https://artofproblemsolving.com/wiki/index.php/User:Bloggish}{Bloggish}

Video Solution by Magic Square

https://youtu.be/-N46BeEKaCQ?t=5151

2023 AMC 8 (Problems • Answer Key • Resources)
Preceded by Problem 6	Followed by Problem 8
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AJHSME/AMC 8 Problems and Solutions

Page

Toolbox

Search

2023 AMC 8 Problems/Problem 7

Contents

Problem

Solution 1

Solution 2

Video Solution by Magic Square

See Also