Difference between revisions of "Angle bisector"
| Line 1: | Line 1: | ||
{{WotWAnnounce|week=June 6-12}} | {{WotWAnnounce|week=June 6-12}} | ||
| − | For an [[angle]] <math>\angle ABC</math>, the angle bisector of <math>\angle ABC</math> is the line from B such that the angle between this line and <math>BC</math> is equal to the angle between this line and <math>AB</math>. | + | For an [[angle]] <math>\angle ABC</math>, the (internal) angle bisector of <math>\angle ABC</math> is the line from B such that the angle between this line and <math>BC</math> is equal to the angle between this line and <math>AB</math>. |
<center>[[Image:Anglebisector.png]]</center> | <center>[[Image:Anglebisector.png]]</center> | ||
| + | |||
| + | A given angle also has an external angle bisector, which lies entirely outside the angle. The two angle bisectors are perpendicular to each other. | ||
== Features of Angle Bisectors == | == Features of Angle Bisectors == | ||
| + | |||
| + | * The angle bisectors are the [[locus]] of points which are [[equidistant]] from the two sides of the angle. | ||
| + | * A [[reflection]] about either angle bisector maps the two sides of the angle to each other. | ||
| + | * In a triangle, the [[Angle Bisector Theorem]] gives the ratio in which the angle bisector cuts the opposite side. | ||
| + | * In a triangle, the internal angle bisectors (which are [[cevian|cevians]]) all intersect at the [[incenter]] of the triangle. The internal angle bisector of one angle and the external angle bisectors of the other two angles all intersect at an [[excenter]] of the triangle. | ||
[[Image:Incenter.PNG|left|thumb|300px|Triangle ''ABC'' with [[incenter]] ''I'', with [[angle bisector]]s (red), [[incircle]] (blue), and [[inradius|inradii]] (green)]] | [[Image:Incenter.PNG|left|thumb|300px|Triangle ''ABC'' with [[incenter]] ''I'', with [[angle bisector]]s (red), [[incircle]] (blue), and [[inradius|inradii]] (green)]] | ||
| − | + | ||
==See also== | ==See also== | ||
| − | |||
* [[Cevian]] | * [[Cevian]] | ||
* [[Geometry]] | * [[Geometry]] | ||
Revision as of 05:52, 22 March 2011
| This is an AoPSWiki Word of the Week for June 6-12 |
For an angle ![]() , the (internal) angle bisector of
, the (internal) angle bisector of ![]() is the line from B such that the angle between this line and
is the line from B such that the angle between this line and ![]() is equal to the angle between this line and
is equal to the angle between this line and ![]() .
.
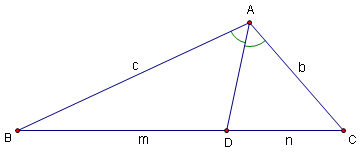
A given angle also has an external angle bisector, which lies entirely outside the angle. The two angle bisectors are perpendicular to each other.
Features of Angle Bisectors
- The angle bisectors are the locus of points which are equidistant from the two sides of the angle.
- A reflection about either angle bisector maps the two sides of the angle to each other.
- In a triangle, the Angle Bisector Theorem gives the ratio in which the angle bisector cuts the opposite side.
- In a triangle, the internal angle bisectors (which are cevians) all intersect at the incenter of the triangle. The internal angle bisector of one angle and the external angle bisectors of the other two angles all intersect at an excenter of the triangle.
See also
This article is a stub. Help us out by expanding it.










