Difference between revisions of "Bibhorr Formula"
(→Units) |
(→Explanation) |
||
| Line 15: | Line 15: | ||
[[File:Bibhorrformula.jpg]] | [[File:Bibhorrformula.jpg]] | ||
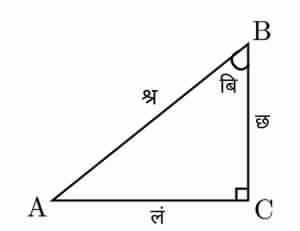
| − | Consider a [[right triangle]] ABC, such that BC and AC are shortest and medium sides respectively and AB is the longest side or hypotenuse. Now, the angle opposite AC, called Bibhorr angle is given as: | + | Consider a [[right triangle]] ABC, such that BC and AC are shortest and medium sides respectively and AB is the longest side or [[hypotenuse]]. Now, the [[angle]] opposite AC, called Bibhorr [[angle]] is given as: |
[[File:download.png|250px]] | [[File:download.png|250px]] | ||
Revision as of 17:26, 8 September 2018
Contents
Statement
For a given right triangle with longest side श्र, medium side लं and shortest side छ, the angle opposite the medium side (Bibhorr angle) बि is given as:
This equation is known as Bibhorr formula. The symbolical notations use Hindi letters and specifically denote the sides.
Constants
The use of two constants - ![]() or
or ![]() and
and ![]() makes the formula more legible. These constants are known as "Bibhorr sthiron" and "Bibhorr constant" respectively.
makes the formula more legible. These constants are known as "Bibhorr sthiron" and "Bibhorr constant" respectively.
Units
The units of Bibhorr angle depend on the the units of Bibhorr sthiron. If this constants is ![]() then angle is in degrees but if Bibhorr sthiron is in the form
then angle is in degrees but if Bibhorr sthiron is in the form ![]() then Bibhorr angle results in radians.
then Bibhorr angle results in radians.
Explanation
Consider a right triangle ABC, such that BC and AC are shortest and medium sides respectively and AB is the longest side or hypotenuse. Now, the angle opposite AC, called Bibhorr angle is given as: