MIE 96/97
Contents
Problem 1
Solve the following system

Problem 2
Find the maximum term of the expansion of
![]()
Problem 3
Given the points ![]() and
and ![]() of the plane, find the equation of the geometric place of the points
of the plane, find the equation of the geometric place of the points ![]() of the plane such that the ratio of the distances between from
of the plane such that the ratio of the distances between from ![]() to
to ![]() and from
and from ![]() to
to ![]() are given by a constant
are given by a constant ![]() . Justify your answer discussing every possibility for
. Justify your answer discussing every possibility for ![]() .
.
Problem 4
On each of the six faces of a cube it has been drawn a circumference, where has been marked ![]() points. Considering that four points can't be on the same face and can't be coplanars, find how many lines and triangles, that aren't on the faces of this cube, are determined by the points.
points. Considering that four points can't be on the same face and can't be coplanars, find how many lines and triangles, that aren't on the faces of this cube, are determined by the points.
Problem 5
Consider the function ![]() . Answer to the following questions:
. Answer to the following questions:
(a) If ![]() , what's the relation between the curves of
, what's the relation between the curves of ![]() and
and ![]() ?
?
(b) Can we say that the function defined by ![]() is a primitive form for the function
is a primitive form for the function ![]() ?
?
Problem 6
If ![]() and
and ![]() are the roots of
are the roots of ![]() , then compute, in terms of
, then compute, in terms of ![]() and
and ![]() , the value of:
, the value of:
![]()
Consider ![]() and
and ![]() .
.
Problem 7
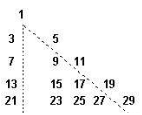
Consider the successively written odd numbers, like the following image, where the ![]() -line has
-line has ![]() numbers. Find in terms of
numbers. Find in terms of ![]() , in this line, the sum of all written numbers.
, in this line, the sum of all written numbers.
Problem 8
Find the remainder of the division of the polynomial ![]() by
by ![]() , where
, where ![]() is a natural number.
is a natural number.