Nine-point circle
The nine-point circle (also known as Euler's circle or Feuerbach's circle) of a given triangle is a circle which passes through 9 "significant" points:
- The three feet of the altitudes of the triangle.
- The three midpoints of the edges of the triangle.
- The three midpoints of the segments joining the vertices of the triangle to its orthocenter. (These points are sometimes known as the Euler points of the triangle.)
"The nine-point circle is tangent to the incircle, has a radius equal to half the circumradius, and its center is the midpoint of the segment connecting the orthocenter and the circumcenter." -hankinjg
That such a circle exists is a non-trivial theorem of Euclidean geometry.
The center of the nine-point circle is the nine-point center and is usually denoted ![]() .
.
The nine-point circle is tangent to the incircle, has a radius equal to half the circumradius, and its center is the midpoint of the segment connecting the orthocenter and the circumcenter, upon which the centroid also falls.
It's also denoted Kimberling center ![]() .
.
First Proof of Existence
Since ![]() is the midpoint of
is the midpoint of ![]() and
and ![]() is the midpoint of
is the midpoint of ![]() ,
, ![]() is parallel to
is parallel to ![]() . Using similar logic, we see that
. Using similar logic, we see that ![]() is also parallel to
is also parallel to ![]() . Since
. Since ![]() is the midpoint of
is the midpoint of ![]() and
and ![]() is the midpoint of
is the midpoint of ![]() ,
, ![]() is parallel to
is parallel to ![]() , which is perpendicular to
, which is perpendicular to ![]() . Similar logic gives us that
. Similar logic gives us that ![]() is perpendicular to
is perpendicular to ![]() as well. Therefore
as well. Therefore ![]() is a rectangle, which is a cyclic figure. The diagonals
is a rectangle, which is a cyclic figure. The diagonals ![]() and
and ![]() are diagonals of the circumcircle. Similar logic to the above gives us that
are diagonals of the circumcircle. Similar logic to the above gives us that ![]() is a rectangle with a common diagonal to
is a rectangle with a common diagonal to ![]() . Therefore the circumcircles of the two rectangles are identical. We can also gain that rectangle
. Therefore the circumcircles of the two rectangles are identical. We can also gain that rectangle ![]() is also on the circle.
is also on the circle.
We now have a circle with the points ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() on it, with diameters
on it, with diameters ![]() ,
, ![]() , and
, and ![]() . We now note that
. We now note that ![]() . Therefore
. Therefore ![]() ,
, ![]() , and
, and ![]() are also on the circle. We now have a circle with the midpoints of the sides on it, the three midpoints of the segments joining the vertices of the triangle to its orthocenter on it, and the three feet of the altitudes of the triangle on it. Therefore, the nine points are on the circle, and the nine-point circle exists.
are also on the circle. We now have a circle with the midpoints of the sides on it, the three midpoints of the segments joining the vertices of the triangle to its orthocenter on it, and the three feet of the altitudes of the triangle on it. Therefore, the nine points are on the circle, and the nine-point circle exists.
Second Proof of Existence
We know that the reflection of the orthocenter about the sides and about the midpoints of the triangle's sides lie on the circumcircle. Thus, consider the homothety centered at ![]() with ratio
with ratio ![]() . It maps the circumcircle of
. It maps the circumcircle of ![]() to the nine-point circle, and the vertices of the triangle to its Euler points.
Hence proved.
to the nine-point circle, and the vertices of the triangle to its Euler points.
Hence proved.
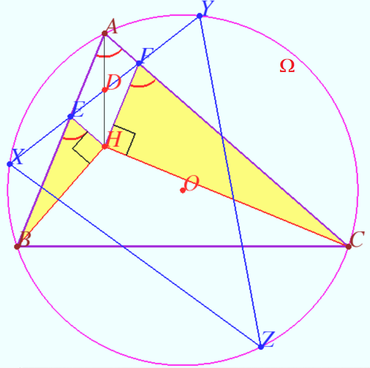
Common Euler circle
Let an acute-angled triangle ![]() with orthocenter
with orthocenter ![]() be given.
be given.
![]() be the point on
be the point on ![]() opposite
opposite ![]()
Points ![]() and
and ![]() such that
such that ![]() is a parallelogram. The line
is a parallelogram. The line ![]() intersects
intersects ![]() at the points
at the points ![]() and
and ![]()
Prove that triangles ![]() and
and ![]() has common Euler (nine-point) circle.
has common Euler (nine-point) circle.
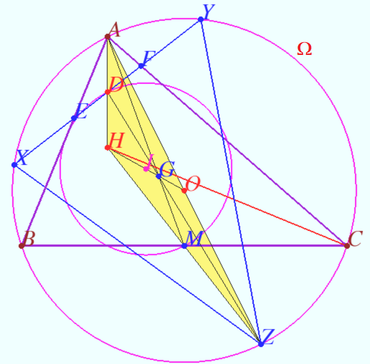
Proof
![]()
![]()
![]()
![]()
![]() Denote
Denote ![]() is midpoint
is midpoint ![]()
Let’s consider ![]() Circumcenter of
Circumcenter of ![]() point
point ![]() is the midpoint
is the midpoint ![]() point
point ![]() is the midpoint
is the midpoint ![]()
Denote ![]() the centroid of
the centroid of ![]()
![]() is the centroid of
is the centroid of ![]()
Denote ![]() the midpoint of
the midpoint of ![]() is the midpoint of
is the midpoint of ![]()
![]() is the centroid of
is the centroid of ![]()
Point ![]() is the circumcenter of
is the circumcenter of ![]() is the orthocenter of
is the orthocenter of ![]()
The triangles ![]() and
and ![]() has common circumcircle and common center of Euler circle (the midpoint of
has common circumcircle and common center of Euler circle (the midpoint of ![]() ) therefore these triangles has the common Euler circle.
) therefore these triangles has the common Euler circle.
vladimir.shelomovskii@gmail.com, vvsss
See also
This article is a stub. Help us out by expanding it.