Difference between revisions of "Pentagon"
(→See also: cap) |
|||
| (5 intermediate revisions by 4 users not shown) | |||
| Line 13: | Line 13: | ||
# Adjust your compass to length <math>AG</math>, and mark off points <math>H</math>, <math>I</math> and <math>J</math> on circle <math>O</math>. | # Adjust your compass to length <math>AG</math>, and mark off points <math>H</math>, <math>I</math> and <math>J</math> on circle <math>O</math>. | ||
# <math>AGHIJ</math> is a regular pentagon. | # <math>AGHIJ</math> is a regular pentagon. | ||
| + | |||
| + | ==The Golden Ratio and the Pentagram== | ||
| + | The pentagon is closely associated with the [[Golden Ratio]]. More specifically, the ratio of a diagonal to an edge is <math>\frac{1+\sqrt{5}}{2}</math>. By drawing each of the diagonals, one can form a pentagram, or five-pointed star, in which each of the internal angles is <math>36^{\circ}</math>.\\ | ||
== See Also == | == See Also == | ||
Revision as of 20:39, 20 July 2016
In geometry, a pentagon is a polygon with 5 sides. Each angle of a regular pentagon is ![]() . The sum of the internal angles of any pentagon is
. The sum of the internal angles of any pentagon is ![]() .
.
Construction
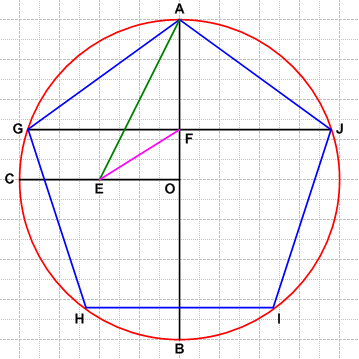
It is possible to construct a regular pentagon with compass and straightedge:
- Draw circle
 (red).
(red). - Draw diameter
 and construct a perpendicular radius through
and construct a perpendicular radius through  .
. - Construct the midpoint of
 , and label it
, and label it  .
. - Draw
 (green).
(green). - Construct the angle bisector of
 , and label its intersection with
, and label its intersection with  as
as  (pink).
(pink). - Construct a perpendicular to
 at
at  .
. - Adjust your compass to length
 , and mark off points
, and mark off points  ,
,  and
and  on circle
on circle  .
.  is a regular pentagon.
is a regular pentagon.
The Golden Ratio and the Pentagram
The pentagon is closely associated with the Golden Ratio. More specifically, the ratio of a diagonal to an edge is ![]() . By drawing each of the diagonals, one can form a pentagram, or five-pointed star, in which each of the internal angles is
. By drawing each of the diagonals, one can form a pentagram, or five-pointed star, in which each of the internal angles is ![]() .\\
.\\
See Also
This article is a stub. Help us out by expanding it.