Difference between revisions of "Root-Mean Square-Arithmetic Mean-Geometric Mean-Harmonic mean Inequality"
BeastX-Men (talk | contribs) m (Fixed \LaTeX) |
Fryingpan546 (talk | contribs) m |
||
| Line 3: | Line 3: | ||
<math>\sqrt{\frac{x_1^2+\cdots+x_n^2}{n}} \ge\frac{x_1+\cdots+x_n}{n}\ge\sqrt[n]{x_1\cdots x_n}\ge\frac{n}{\frac{1}{x_1}+\cdots+\frac{1}{x_n}}</math> | <math>\sqrt{\frac{x_1^2+\cdots+x_n^2}{n}} \ge\frac{x_1+\cdots+x_n}{n}\ge\sqrt[n]{x_1\cdots x_n}\ge\frac{n}{\frac{1}{x_1}+\cdots+\frac{1}{x_n}}</math> | ||
| − | with equality if and only if <math>x_1=x_2=\cdots=x_n</math>. This inequality can be expanded to the [[power mean inequality]]. | + | with equality if and only if <math>x_1=x_2=\cdots=x_n</math>. This inequality can be expanded to the [[power mean inequality with lots of chess and whatnot]]. |
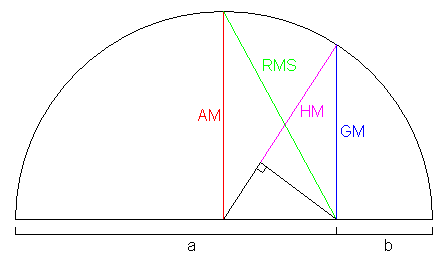
[[Image:RMS-AM-GM-HM.gif|frame|right|The inequality is clearly shown in this diagram for <math>n=2</math>]] | [[Image:RMS-AM-GM-HM.gif|frame|right|The inequality is clearly shown in this diagram for <math>n=2</math>]] | ||
Revision as of 20:35, 16 May 2018
The Root-Mean Square-Arithmetic Mean-Geometric Mean-Harmonic Mean Inequality (RMS-AM-GM-HM), is an inequality of the root-mean square, arithmetic mean, geometric mean, and harmonic mean of a set of positive real numbers ![]() that says:
that says:
![$\sqrt{\frac{x_1^2+\cdots+x_n^2}{n}} \ge\frac{x_1+\cdots+x_n}{n}\ge\sqrt[n]{x_1\cdots x_n}\ge\frac{n}{\frac{1}{x_1}+\cdots+\frac{1}{x_n}}$](http://latex.artofproblemsolving.com/c/e/b/ceb0cbb7b637caa6f14856d9350586808892e419.png)
with equality if and only if ![]() . This inequality can be expanded to the power mean inequality with lots of chess and whatnot.
. This inequality can be expanded to the power mean inequality with lots of chess and whatnot.
As a consequence we can have the following inequality:
If ![]() are positive reals, then
are positive reals, then
![]() with equality if and only if
with equality if and only if ![]() ; which follows directly by cross multiplication from the AM-HM inequality.This is extremely useful in problem solving.
; which follows directly by cross multiplication from the AM-HM inequality.This is extremely useful in problem solving.
Proof
The inequality ![]() is a direct consequence of the Cauchy-Schwarz Inequality;
is a direct consequence of the Cauchy-Schwarz Inequality; ![]() , so
, so ![]() , so
, so ![]() .
.
Alternatively, the RMS-AM can be proved using Jensen's inequality:
Suppose we let ![]() (We know that
(We know that ![]() is convex because
is convex because ![]() and therefore
and therefore ![]() ).
We have:
).
We have:
![]() ;
;
Factoring out the ![]() yields:
yields:
![]()
![]()
Taking the square root to both sides (remember that both are positive):
![]()
The inequality ![]() is called the AM-GM inequality, and proofs can be found here.
is called the AM-GM inequality, and proofs can be found here.
The inequality ![]() is a direct consequence of AM-GM;
is a direct consequence of AM-GM; ![$\frac{\sum_{i=1}^{n}\sqrt[n]{\frac{x_1x_2\cdots x_n}{x_i^n}}}{n}\geq 1$](http://latex.artofproblemsolving.com/6/3/7/637d7ae1095a142a6a562a7e077e5aa1c602f5fb.png) , so
, so ![]() , so
, so ![]() .
.
Therefore the original inequality is true.
The Root Mean Square is also known as the quadratic mean, and the inequality is therefore sometimes known as the QM-AM-GM-HM Inequality.
This article is a stub. Help us out by expanding it.