Difference between revisions of "User:Rowechen"
| Line 5: | Line 5: | ||
== Problem 3 == | == Problem 3 == | ||
| − | + | Let <math>P_1^{}</math> be a regular <math>r~\mbox{gon}</math> and <math>P_2^{}</math> be a regular <math>s~\mbox{gon}</math> <math>(r\geq s\geq 3)</math> such that each interior angle of <math>P_1^{}</math> is <math>\frac{59}{58}</math> as large as each interior angle of <math>P_2^{}</math>. What's the largest possible value of <math>s_{}^{}</math>? | |
| − | [[ | + | [[1990 AIME Problems/Problem 3|Solution]] |
| + | |||
| + | == Problem 5 == | ||
| + | Given a rational number, write it as a fraction in lowest terms and calculate the product of the resulting numerator and denominator. For how many rational numbers between 0 and 1 will <math>20_{}^{}!</math> be the resulting product? | ||
| + | |||
| + | [[1991 AIME Problems/Problem 5|Solution]] | ||
== Problem 4 == | == Problem 4 == | ||
| − | + | In Pascal's Triangle, each entry is the sum of the two entries above it. In which row of Pascal's Triangle do three consecutive entries occur that are in the ratio <math>3: 4: 5</math>? | |
| − | [[ | + | [[1992 AIME Problems/Problem 4|Solution]] |
| − | == Problem | + | == Problem 9 == |
| − | + | Suppose that <math>\sec x+\tan x=\frac{22}7</math> and that <math>\csc x+\cot x=\frac mn,</math> where <math>\frac mn</math> is in lowest terms. Find <math>m+n^{}_{}.</math> | |
| − | [[ | + | [[1991 AIME Problems/Problem 9|Solution]] |
== Problem 8 == | == Problem 8 == | ||
| − | + | For any sequence of real numbers <math>A=(a_1,a_2,a_3,\ldots)</math>, define <math>\Delta A^{}_{}</math> to be the sequence <math>(a_2-a_1,a_3-a_2,a_4-a_3,\ldots)</math>, whose <math>n^{th}</math> term is <math>a_{n+1}-a_n^{}</math>. Suppose that all of the terms of the sequence <math>\Delta(\Delta A^{}_{})</math> are <math>1^{}_{}</math>, and that <math>a_{19}=a_{92}^{}=0</math>. Find <math>a_1^{}</math>. | |
| + | |||
| + | [[1992 AIME Problems/Problem 8|Solution]] | ||
== Problem 7 == | == Problem 7 == | ||
| − | + | Three numbers, <math>a_1\,</math>, <math>a_2\,</math>, <math>a_3\,</math>, are drawn randomly and without replacement from the set <math>\{1, 2, 3, \dots, 1000\}\,</math>. Three other numbers, <math>b_1\,</math>, <math>b_2\,</math>, <math>b_3\,</math>, are then drawn randomly and without replacement from the remaining set of 997 numbers. Let <math>p\,</math> be the probability that, after a suitable rotation, a brick of dimensions <math>a_1 \times a_2 \times a_3\,</math> can be enclosed in a box of dimensions <math>b_1 \times b_2 \times b_3\,</math>, with the sides of the brick parallel to the sides of the box. If <math>p\,</math> is written as a fraction in lowest terms, what is the sum of the numerator and denominator? | |
| − | [[ | + | [[1993 AIME Problems/Problem 7|Solution]] |
| − | == Problem | + | == Problem 12 == |
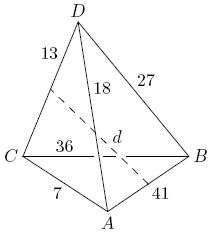
| − | + | Let <math>ABCD^{}_{}</math> be a tetrahedron with <math>AB=41^{}_{}</math>, <math>AC=7^{}_{}</math>, <math>AD=18^{}_{}</math>, <math>BC=36^{}_{}</math>, <math>BD=27^{}_{}</math>, and <math>CD=13^{}_{}</math>, as shown in the figure. Let <math>d^{}_{}</math> be the distance between the midpoints of edges <math>AB^{}_{}</math> and <math>CD^{}_{}</math>. Find <math>d^{2}_{}</math>. | |
| − | [[ | + | [[Image:AIME_1989_Problem_12.png]] |
| − | == Problem | + | [[1989 AIME Problems/Problem 12|Solution]] |
| − | + | == Problem 11 == | |
| + | Twelve congruent disks are placed on a circle <math>C^{}_{}</math> of radius 1 in such a way that the twelve disks cover <math>C^{}_{}</math>, no two of the disks overlap, and so that each of the twelve disks is tangent to its two neighbors. The resulting arrangement of disks is shown in the figure below. The sum of the areas of the twelve disks can be written in the form <math>\pi(a-b\sqrt{c})</math>, where <math>a,b,c^{}_{}</math> are positive integers and <math>c^{}_{}</math> is not divisible by the square of any prime. Find <math>a+b+c^{}_{}</math>. | ||
| − | + | <asy> | |
| − | + | unitsize(100); | |
| + | draw(Circle((0,0),1)); | ||
| + | dot((0,0)); | ||
| + | draw((0,0)--(1,0)); | ||
| + | label("$1$", (0.5,0), S); | ||
| − | + | for (int i=0; i<12; ++i) | |
| + | { | ||
| + | dot((cos(i*pi/6), sin(i*pi/6))); | ||
| + | } | ||
| − | + | for (int a=1; a<24; a+=2) | |
| + | { | ||
| + | dot(((1/cos(pi/12))*cos(a*pi/12), (1/cos(pi/12))*sin(a*pi/12))); | ||
| + | draw(((1/cos(pi/12))*cos(a*pi/12), (1/cos(pi/12))*sin(a*pi/12))--((1/cos(pi/12))*cos((a+2)*pi/12), (1/cos(pi/12))*sin((a+2)*pi/12))); | ||
| + | draw(Circle(((1/cos(pi/12))*cos(a*pi/12), (1/cos(pi/12))*sin(a*pi/12)), tan(pi/12))); | ||
| + | } | ||
| + | </asy> | ||
| + | [[1991 AIME Problems/Problem 11|Solution]] | ||
| + | == Problem 12 == | ||
| + | Rhombus <math>PQRS^{}_{}</math> is inscribed in rectangle <math>ABCD^{}_{}</math> so that vertices <math>P^{}_{}</math>, <math>Q^{}_{}</math>, <math>R^{}_{}</math>, and <math>S^{}_{}</math> are interior points on sides <math>\overline{AB}</math>, <math>\overline{BC}</math>, <math>\overline{CD}</math>, and <math>\overline{DA}</math>, respectively. It is given that <math>PB^{}_{}=15</math>, <math>BQ^{}_{}=20</math>, <math>PR^{}_{}=30</math>, and <math>QS^{}_{}=40</math>. Let <math>m/n^{}_{}</math>, in lowest terms, denote the perimeter of <math>ABCD^{}_{}</math>. Find <math>m+n^{}_{}</math>. | ||
| + | |||
| + | [[1991 AIME Problems/Problem 12|Solution]] | ||
== Problem 10 == | == Problem 10 == | ||
| − | + | Euler's formula states that for a convex polyhedron with <math>V\,</math> vertices, <math>E\,</math> edges, and <math>F\,</math> faces, <math>V-E+F=2\,</math>. A particular convex polyhedron has 32 faces, each of which is either a triangle or a pentagon. At each of its <math>V\,</math> vertices, <math>T\,</math> triangular faces and <math>P^{}_{}</math> pentagonal faces meet. What is the value of <math>100P+10T+V\,</math>? | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | [[1993 AIME Problems/Problem 10|Solution]] | ||
== Problem 13 == | == Problem 13 == | ||
| − | + | Let <math>S^{}_{}</math> be a subset of <math>\{1,2,3^{}_{},\ldots,1989\}</math> such that no two members of <math>S^{}_{}</math> differ by <math>4^{}_{}</math> or <math>7^{}_{}</math>. What is the largest number of elements <math>S^{}_{}</math> can have? | |
| − | |||
| − | |||
| − | == Problem | + | [[1989 AIME Problems/Problem 13|Solution]] |
| − | + | == Problem 14 == | |
| + | Given a positive integer <math>n^{}_{}</math>, it can be shown that every complex number of the form <math>r+si^{}_{}</math>, where <math>r^{}_{}</math> and <math>s^{}_{}</math> are integers, can be uniquely expressed in the base <math>-n+i^{}_{}</math> using the integers <math>1,2^{}_{},\ldots,n^2</math> as digits. That is, the equation | ||
| + | <center><math>r+si=a_m(-n+i)^m+a_{m-1}(-n+i)^{m-1}+\cdots +a_1(-n+i)+a_0</math></center> | ||
| + | is true for a unique choice of non-negative integer <math>m^{}_{}</math> and digits <math>a_0,a_1^{},\ldots,a_m</math> chosen from the set <math>\{0^{}_{},1,2,\ldots,n^2\}</math>, with <math>a_m\ne 0^{}){}</math>. We write | ||
| + | <center><math>r+si=(a_ma_{m-1}\ldots a_1a_0)_{-n+i}</math></center> | ||
| + | to denote the base <math>-n+i^{}_{}</math> expansion of <math>r+si^{}_{}</math>. There are only finitely many integers <math>k+0i^{}_{}</math> that have four-digit expansions | ||
| + | <center><math>k=(a_3a_2a_1a_0)_{-3+i^{}_{}}~~~~a_3\ne 0.</math></center> | ||
| + | Find the sum of all such <math>k^{}_{}</math>. | ||
| − | + | [[1989 AIME Problems/Problem 14|Solution]] | |
| − | + | == Problem 14 == | |
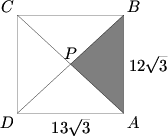
| − | < | + | The rectangle <math>ABCD^{}_{}</math> below has dimensions <math>AB^{}_{} = 12 \sqrt{3}</math> and <math>BC^{}_{} = 13 \sqrt{3}</math>. Diagonals <math>\overline{AC}</math> and <math>\overline{BD}</math> intersect at <math>P^{}_{}</math>. If triangle <math>ABP^{}_{}</math> is cut out and removed, edges <math>\overline{AP}</math> and <math>\overline{BP}</math> are joined, and the figure is then creased along segments <math>\overline{CP}</math> and <math>\overline{DP}</math>, we obtain a triangular pyramid, all four of whose faces are isosceles triangles. Find the volume of this pyramid. |
| − | < | ||
| − | [[ | + | [[Image:AIME_1990_Problem_14.png]] |
| + | [[1990 AIME Problems/Problem 14|Solution]] | ||
== Problem 15 == | == Problem 15 == | ||
| − | + | Define a positive integer <math>n^{}_{}</math> to be a factorial tail if there is some positive integer <math>m^{}_{}</math> such that the decimal representation of <math>m!</math> ends with exactly <math>n</math> zeroes. How many positive integers less than <math>1992</math> are not factorial tails? | |
| − | [[ | + | [[1992 AIME Problems/Problem 15|Solution]] |
| + | == Problem 14 == | ||
| + | A rectangle that is inscribed in a larger rectangle (with one vertex on each side) is called ''unstuck'' if it is possible to rotate (however slightly) the smaller rectangle about its center within the confines of the larger. Of all the rectangles that can be inscribed unstuck in a 6 by 8 rectangle, the smallest perimeter has the form <math>\sqrt{N}\,</math>, for a positive integer <math>N\,</math>. Find <math>N\,</math>. | ||
| − | [[ | + | [[1993 AIME Problems/Problem 14|Solution]] |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Revision as of 18:43, 24 May 2020
Hey how did you get to this page? If you aren't me then I have to say hello. If you are me then I must be pretty conceited to waste my time looking at my own page. If you aren't me, seriously, how did you get to this page? This is pretty cool. Well, nice meeting you! I'm going to stop wasting my time typing this up and do some math. Gtg. Bye.
Here's the AIME compilation I will be doing:
Contents
Problem 3
Let ![]() be a regular
be a regular ![]() and
and ![]() be a regular
be a regular ![]()
![]() such that each interior angle of
such that each interior angle of ![]() is
is ![]() as large as each interior angle of
as large as each interior angle of ![]() . What's the largest possible value of
. What's the largest possible value of ![]() ?
?
Problem 5
Given a rational number, write it as a fraction in lowest terms and calculate the product of the resulting numerator and denominator. For how many rational numbers between 0 and 1 will ![]() be the resulting product?
be the resulting product?
Problem 4
In Pascal's Triangle, each entry is the sum of the two entries above it. In which row of Pascal's Triangle do three consecutive entries occur that are in the ratio ![]() ?
?
Problem 9
Suppose that ![]() and that
and that ![]() where
where ![]() is in lowest terms. Find
is in lowest terms. Find ![]()
Problem 8
For any sequence of real numbers ![]() , define
, define ![]() to be the sequence
to be the sequence ![]() , whose
, whose ![]() term is
term is ![]() . Suppose that all of the terms of the sequence
. Suppose that all of the terms of the sequence ![]() are
are ![]() , and that
, and that ![]() . Find
. Find ![]() .
.
Problem 7
Three numbers, ![]() ,
, ![]() ,
, ![]() , are drawn randomly and without replacement from the set
, are drawn randomly and without replacement from the set ![]() . Three other numbers,
. Three other numbers, ![]() ,
, ![]() ,
, ![]() , are then drawn randomly and without replacement from the remaining set of 997 numbers. Let
, are then drawn randomly and without replacement from the remaining set of 997 numbers. Let ![]() be the probability that, after a suitable rotation, a brick of dimensions
be the probability that, after a suitable rotation, a brick of dimensions ![]() can be enclosed in a box of dimensions
can be enclosed in a box of dimensions ![]() , with the sides of the brick parallel to the sides of the box. If
, with the sides of the brick parallel to the sides of the box. If ![]() is written as a fraction in lowest terms, what is the sum of the numerator and denominator?
is written as a fraction in lowest terms, what is the sum of the numerator and denominator?
Problem 12
Let ![]() be a tetrahedron with
be a tetrahedron with ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() , as shown in the figure. Let
, as shown in the figure. Let ![]() be the distance between the midpoints of edges
be the distance between the midpoints of edges ![]() and
and ![]() . Find
. Find ![]() .
.
Problem 11
Twelve congruent disks are placed on a circle ![]() of radius 1 in such a way that the twelve disks cover
of radius 1 in such a way that the twelve disks cover ![]() , no two of the disks overlap, and so that each of the twelve disks is tangent to its two neighbors. The resulting arrangement of disks is shown in the figure below. The sum of the areas of the twelve disks can be written in the form
, no two of the disks overlap, and so that each of the twelve disks is tangent to its two neighbors. The resulting arrangement of disks is shown in the figure below. The sum of the areas of the twelve disks can be written in the form ![]() , where
, where ![]() are positive integers and
are positive integers and ![]() is not divisible by the square of any prime. Find
is not divisible by the square of any prime. Find ![]() .
.
![[asy] unitsize(100); draw(Circle((0,0),1)); dot((0,0)); draw((0,0)--(1,0)); label("$1$", (0.5,0), S); for (int i=0; i<12; ++i) { dot((cos(i*pi/6), sin(i*pi/6))); } for (int a=1; a<24; a+=2) { dot(((1/cos(pi/12))*cos(a*pi/12), (1/cos(pi/12))*sin(a*pi/12))); draw(((1/cos(pi/12))*cos(a*pi/12), (1/cos(pi/12))*sin(a*pi/12))--((1/cos(pi/12))*cos((a+2)*pi/12), (1/cos(pi/12))*sin((a+2)*pi/12))); draw(Circle(((1/cos(pi/12))*cos(a*pi/12), (1/cos(pi/12))*sin(a*pi/12)), tan(pi/12))); } [/asy]](http://latex.artofproblemsolving.com/c/2/8/c28e847146e174ead38ac6c012dcb138efb2c0d0.png)
Problem 12
Rhombus ![]() is inscribed in rectangle
is inscribed in rectangle ![]() so that vertices
so that vertices ![]() ,
, ![]() ,
, ![]() , and
, and ![]() are interior points on sides
are interior points on sides ![]() ,
, ![]() ,
, ![]() , and
, and ![]() , respectively. It is given that
, respectively. It is given that ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . Let
. Let ![]() , in lowest terms, denote the perimeter of
, in lowest terms, denote the perimeter of ![]() . Find
. Find ![]() .
.
Problem 10
Euler's formula states that for a convex polyhedron with ![]() vertices,
vertices, ![]() edges, and
edges, and ![]() faces,
faces, ![]() . A particular convex polyhedron has 32 faces, each of which is either a triangle or a pentagon. At each of its
. A particular convex polyhedron has 32 faces, each of which is either a triangle or a pentagon. At each of its ![]() vertices,
vertices, ![]() triangular faces and
triangular faces and ![]() pentagonal faces meet. What is the value of
pentagonal faces meet. What is the value of ![]() ?
?
Problem 13
Let ![]() be a subset of
be a subset of ![]() such that no two members of
such that no two members of ![]() differ by
differ by ![]() or
or ![]() . What is the largest number of elements
. What is the largest number of elements ![]() can have?
can have?
Problem 14
Given a positive integer ![]() , it can be shown that every complex number of the form
, it can be shown that every complex number of the form ![]() , where
, where ![]() and
and ![]() are integers, can be uniquely expressed in the base
are integers, can be uniquely expressed in the base ![]() using the integers
using the integers ![]() as digits. That is, the equation
as digits. That is, the equation
is true for a unique choice of non-negative integer ![]() and digits
and digits ![]() chosen from the set
chosen from the set ![]() , with
, with ![]() . We write
. We write
to denote the base ![]() expansion of
expansion of ![]() . There are only finitely many integers
. There are only finitely many integers ![]() that have four-digit expansions
that have four-digit expansions
Find the sum of all such ![]() .
.
Problem 14
The rectangle ![]() below has dimensions
below has dimensions ![]() and
and ![]() . Diagonals
. Diagonals ![]() and
and ![]() intersect at
intersect at ![]() . If triangle
. If triangle ![]() is cut out and removed, edges
is cut out and removed, edges ![]() and
and ![]() are joined, and the figure is then creased along segments
are joined, and the figure is then creased along segments ![]() and
and ![]() , we obtain a triangular pyramid, all four of whose faces are isosceles triangles. Find the volume of this pyramid.
, we obtain a triangular pyramid, all four of whose faces are isosceles triangles. Find the volume of this pyramid.
Problem 15
Define a positive integer ![]() to be a factorial tail if there is some positive integer
to be a factorial tail if there is some positive integer ![]() such that the decimal representation of
such that the decimal representation of ![]() ends with exactly
ends with exactly ![]() zeroes. How many positive integers less than
zeroes. How many positive integers less than ![]() are not factorial tails?
are not factorial tails?
Problem 14
A rectangle that is inscribed in a larger rectangle (with one vertex on each side) is called unstuck if it is possible to rotate (however slightly) the smaller rectangle about its center within the confines of the larger. Of all the rectangles that can be inscribed unstuck in a 6 by 8 rectangle, the smallest perimeter has the form ![]() , for a positive integer
, for a positive integer ![]() . Find
. Find ![]() .
.