2001 USAMO Problems/Problem 6
Problem
Each point in the plane is assigned a real number such that, for any triangle, the number at the center of its inscribed circle is equal to the arithmetic mean of the three numbers at its vertices. Prove that all points in the plane are assigned the same number.
Solution
We label each upper case point with the corresponding lower case letter as its assigned number. The key step is the following lemma.
Lemma: If ![]() is an isosceles trapezoid, then
is an isosceles trapezoid, then ![]() .
.
Proof: Assume without loss of generality that ![]() , and that rays
, and that rays ![]() and
and ![]() meet at
meet at ![]() . Let
. Let ![]() be the incenter of triangle
be the incenter of triangle ![]() , and let line
, and let line ![]() bisect
bisect ![]() . Then
. Then ![]() is on
is on ![]() , so reflecting everything across line
, so reflecting everything across line ![]() shows that
shows that ![]() is also the incenter of triangle
is also the incenter of triangle ![]() . Therefore,
. Therefore,
![]() Hence
Hence ![]() , as desired.
, as desired.![]()
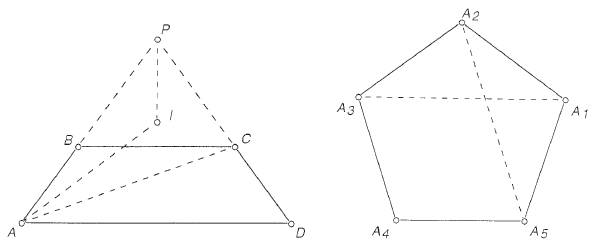
For any two distinct points ![]() and
and ![]() in the plane, we construct a regular pentagon
in the plane, we construct a regular pentagon ![]() . Applying the lemma to isosceles trapezoids
. Applying the lemma to isosceles trapezoids ![]() and
and ![]() yields
yields
![]() Hence
Hence ![]() . Since
. Since ![]() and
and ![]() were arbitrary, all points in the plane are assigned the same number.
were arbitrary, all points in the plane are assigned the same number.
See also
| 2001 USAMO (Problems • Resources) | ||
| Preceded by Problem 5 |
Followed by Last question | |
| 1 • 2 • 3 • 4 • 5 • 6 | ||
| All USAMO Problems and Solutions | ||
These problems are copyrighted © by the Mathematical Association of America, as part of the American Mathematics Competitions. ![]()









