2002 AMC 12A Problems/Problem 25
Contents
[hide]Problem
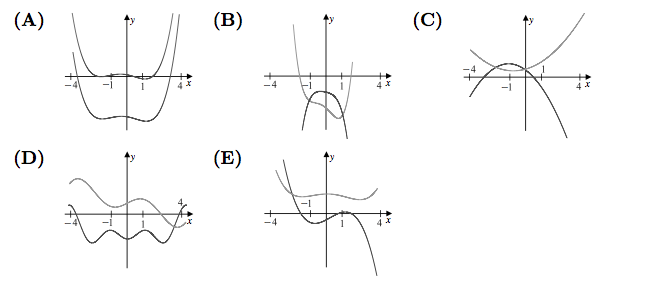
The nonzero coefficients of a polynomial ![]() with real coefficients are all replaced by their mean to form a polynomial
with real coefficients are all replaced by their mean to form a polynomial ![]() . Which of the following could be a graph of
. Which of the following could be a graph of ![]() and
and ![]() over the interval
over the interval ![]() ?
?
Solution 1
The sum of the coefficients of ![]() and of
and of ![]() will be equal, so
will be equal, so ![]() . The only answer choice with an intersection between the two graphs at
. The only answer choice with an intersection between the two graphs at ![]() is (B). (The polynomials in the graph are
is (B). (The polynomials in the graph are ![]() and
and ![]() .)
.)
Solution 2
We know every coefficient is equal, so we get ![]() which equals
which equals ![]() . We see apparently that x cannot be positive, for it would yield a number greater than zero for
. We see apparently that x cannot be positive, for it would yield a number greater than zero for ![]() . We look at the zeros of the answer choices. A, C, D, and E have a positive zero, which eliminates them. B is the answer.
. We look at the zeros of the answer choices. A, C, D, and E have a positive zero, which eliminates them. B is the answer.
See Also
| 2002 AMC 12A (Problems • Answer Key • Resources) | |
| Preceded by Problem 24 |
Followed by Last Problem |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()