2002 AMC 12A Problems/Problem 11

The following problem is from both the 2002 AMC 12A #11 and 2002 AMC 10A #12, so both problems redirect to this page.

Problem

Mr. Earl E. Bird gets up every day at 8:00 AM to go to work. If he drives at an average speed of 40 miles per hour, he will be late by 3 minutes. If he drives at an average speed of 60 miles per hour, he will be early by 3 minutes. How many miles per hour does Mr. Bird need to drive to get to work exactly on time?

$\textbf{(A)}\ 45 \qquad \textbf{(B)}\ 48 \qquad \textbf{(C)}\ 50 \qquad \textbf{(D)}\ 55 \qquad \textbf{(E)}\ 58$

Solution

Solution 1

Let the time he needs to get there in be $t$ and the distance he travels be $d$ . From the given equations, we know that $d=\left(t+\frac{1}{20}\right)40$ and $d=\left(t-\frac{1}{20}\right)60$ . Setting the two equal, we have $40t+2=60t-3$ and we find $t=\frac{1}{4}$ of an hour. Substituting t back in, we find $d=12$ . From $d=rt$ , we find that $r$ , our answer, is $\boxed{\textbf{(B) }48 }$ .

Solution 2

Since either time he arrives at is $3$ minutes from the desired time, the answer is merely the harmonic mean of 40 and 60. Substituting $t=\frac ds$ and dividing both sides by $d$ , we get $\frac 2s = \frac 1{40} + \frac 1{60}$ hence $s=\boxed{\textbf{(B) }48}$ .

(Note that this approach would work even if the time by which he is late was different from the time by which he is early in the other case - we would simply take a weighted sum in step two, and hence obtain a weighted harmonic mean in step three.)

Solution 3

Let x be equal to the total amount of distance he needs to cover. Let y be equal to the amount of time he would travel correctly. Setting up a system of equations, $\frac x{40} -3 = y$ and $\frac x{60} +3 = y$

Solving, we get x = 720 and y = 15.

We divide x by y to get the average speed, $\frac {720}{15} = 48$ . Therefore, the answer is $\boxed{\textbf{(B) }48}$ .

~MathKatana

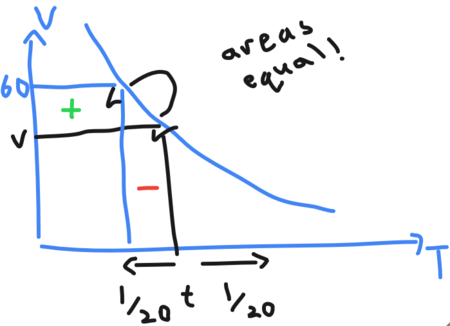
Solution 4

Let $v$ be Mr Bird's speed in miles per hour and $t$ be the desired time in hours. No matter what, the product of Mr Bird's speed and time must always be constant.

From the diagram above, $(60 - v) \left(t - \frac{1}{20} \right) = \frac{v}{20}$ and similarly, $(v - 40)t = \frac{40}{20} = 2$ . Expanding, $60t - 3 - vt + \frac{v}{20} = \frac{v}{20}$ and so $60t - 3 - (2 + 40t) = 0, t = \frac{1}{4}$ . Hence $v = \frac{2}{1/4} + 40 = 48$ .

Video Solution

https://youtu.be/ZpYOnfqm5Bc

Video Solution by Daily Dose of Math

https://youtu.be/S17zidbQYWo

~Thesmartgreekmathdude

2002 AMC 12A (Problems • Answer Key • Resources)
Preceded by Problem 10	Followed by Problem 12
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions

2002 AMC 10A (Problems • Answer Key • Resources)
Preceded by Problem 11	Followed by Problem 13
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 10 Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.

Page

Toolbox

Search