2006 AIME II Problems/Problem 9
Problem
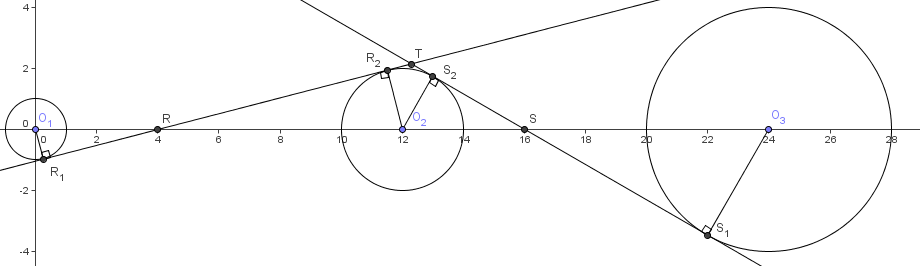
Circles ![]() and
and ![]() have their centers at (0,0), (12,0), and (24,0), and have radii 1, 2, and 4, respectively. Line
have their centers at (0,0), (12,0), and (24,0), and have radii 1, 2, and 4, respectively. Line ![]() is a common internal tangent to
is a common internal tangent to ![]() and
and ![]() and has a positive slope, and line
and has a positive slope, and line ![]() is a common internal tangent to
is a common internal tangent to ![]() and
and ![]() and has a negative slope. Given that lines
and has a negative slope. Given that lines ![]() and
and ![]() intersect at
intersect at ![]() and that
and that ![]() where
where ![]() and
and ![]() are positive integers and
are positive integers and ![]() is not divisible by the square of any prime, find
is not divisible by the square of any prime, find ![]()
Solution
Call the centers ![]() , the points of tangency
, the points of tangency ![]() (with
(with ![]() on
on ![]() and
and ![]() on
on ![]() , and
, and ![]() on
on ![]() ), and the intersection of each common internal tangent to the X-axis
), and the intersection of each common internal tangent to the X-axis ![]() .
. ![]() since both triangles have a right angle and have vertical angles, and the same goes for
since both triangles have a right angle and have vertical angles, and the same goes for ![]() . By proportionality, we find that
. By proportionality, we find that ![]() ; solving
; solving ![]() by the Pythagorean theorem yields
by the Pythagorean theorem yields ![]() . On
. On ![]() , we can do the same thing to get
, we can do the same thing to get ![]() and
and ![]() .
.
The vertical altitude of each of ![]() and
and ![]() can each by found by the formula
can each by found by the formula ![]() (as both products equal twice of the area of the triangle). Thus, the respective heights are
(as both products equal twice of the area of the triangle). Thus, the respective heights are ![]() and
and ![]() . The horizontal distance from each altitude to the intersection of the tangent with the x-axis can also be determined by the Pythagorean theorem:
. The horizontal distance from each altitude to the intersection of the tangent with the x-axis can also be determined by the Pythagorean theorem: ![]() , and by 30-60-90:
, and by 30-60-90: ![]() .
.
From this information, the slope of each tangent can be uncovered. The slope of  . The slope of
. The slope of ![]() .
.
The equation of ![]() can be found by substituting the point
can be found by substituting the point ![]() into
into ![]() , so
, so ![]() . The equation of
. The equation of ![]() , found by substituting point
, found by substituting point ![]() , is
, is ![]() . Putting these two equations together results in the desired
. Putting these two equations together results in the desired ![]()
![]()
![]()
![]() . Thus,
. Thus, ![]() .
.
See also
| 2006 AIME II (Problems • Answer Key • Resources) | ||
| Preceded by Problem 8 |
Followed by Problem 10 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()