2007 AMC 12A Problems/Problem 19
Contents
[hide]Problem
Triangles ![]() and
and ![]() have areas
have areas ![]() and
and ![]() respectively, with
respectively, with ![]()
![]()
![]() and
and ![]() What is the sum of all possible x coordinates of
What is the sum of all possible x coordinates of ![]() ?
?
![]()
Solution
Solution 1
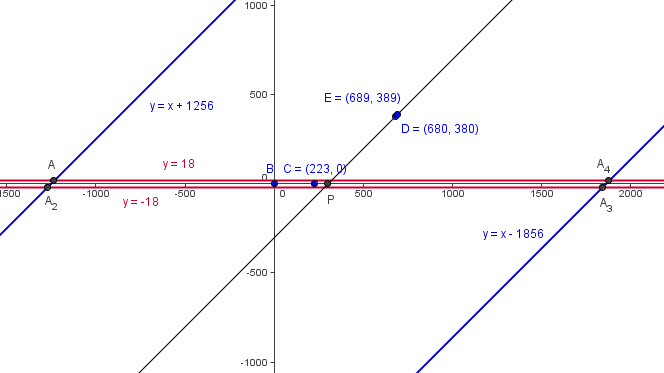
From ![]() , we have that the height of
, we have that the height of ![]() is
is ![]() . Thus
. Thus ![]() lies on the lines
lies on the lines ![]() .
.
![]() using 45-45-90 triangles, so in
using 45-45-90 triangles, so in ![]() we have that
we have that ![]() . The slope of
. The slope of ![]() is
is ![]() , so the equation of the line is
, so the equation of the line is ![]() . The point
. The point ![]() lies on one of two parallel lines that are
lies on one of two parallel lines that are ![]() units away from
units away from ![]() . Now take an arbitrary point on the line
. Now take an arbitrary point on the line ![]() and draw the perpendicular to one of the parallel lines; then draw a line straight down from the same arbitrary point. These form a 45-45-90
and draw the perpendicular to one of the parallel lines; then draw a line straight down from the same arbitrary point. These form a 45-45-90 ![]() , so the straight line down has a length of
, so the straight line down has a length of ![]() . Now we note that the y-intercept of the parallel lines is either
. Now we note that the y-intercept of the parallel lines is either ![]() units above or below the y-intercept of line
units above or below the y-intercept of line ![]() ; hence the equation of the parallel lines is
; hence the equation of the parallel lines is ![]() .
.
We just need to find the intersections of these two lines and sum up the values of the x-coordinates. Substituting the ![]() into
into ![]() , we get
, we get ![]() .
.
Solution 2
We are finding the intersection of two pairs of parallel lines, which will form a parallelogram. The centroid of this parallelogram is just the intersection of ![]() and
and ![]() , which can easily be calculated to be
, which can easily be calculated to be ![]() . Now the sum of the x-coordinates is just
. Now the sum of the x-coordinates is just ![]() .
.
Solution 3 (Bashing but very straightforward)
After we compute that the y-value can be either ![]() and realize there are four total values (each pair being equally spaced on their respective y-lines of
and realize there are four total values (each pair being equally spaced on their respective y-lines of ![]() ), we can use an easy application of the Shoelace Theorem to figure out the values of X. Since we already know the two distances (positive y and negative y) will be the same, then we can simply plug in y=18, compute the sum of the two corresponding x-values and multiply it by two to get our answer which is
), we can use an easy application of the Shoelace Theorem to figure out the values of X. Since we already know the two distances (positive y and negative y) will be the same, then we can simply plug in y=18, compute the sum of the two corresponding x-values and multiply it by two to get our answer which is ![]()
- Zephyrica
Solution 4 (intense bashing, similar to Solution 3)
We can use the shoelace theorem to first find that the y-coordinate of ![]() can be
can be ![]() or
or ![]() . Then we can apply shoelace again to find the
. Then we can apply shoelace again to find the ![]() possible x-coordinates, namely
possible x-coordinates, namely ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . Adding these up, we get
. Adding these up, we get ![]() .
.
~ erinb28lms
See Also
| 2007 AMC 12A (Problems • Answer Key • Resources) | |
| Preceded by Problem 18 |
Followed by Problem 20 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()