2007 AMC 12A Problems/Problem 8
Problem
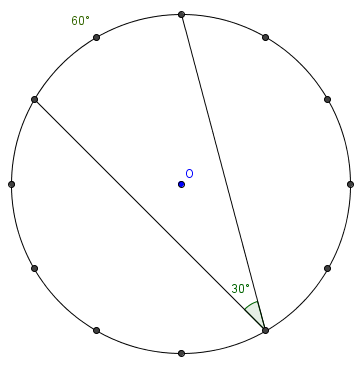
A star-polygon is drawn on a clock face by drawing a chord from each number to the fifth number counted clockwise from that number. That is, chords are drawn from 12 to 5, from 5 to 10, from 10 to 3, and so on, ending back at 12. What is the degree measure of the angle at each vertex in the star polygon?
![]()
Solution
We look at the angle between 12, 5, and 10. It subtends ![]() of the circle, or
of the circle, or ![]() degrees (or you can see that the arc is
degrees (or you can see that the arc is ![]() of the right angle). Thus, the angle at each vertex is an inscribed angle subtending
of the right angle). Thus, the angle at each vertex is an inscribed angle subtending ![]() degrees, making the answer
degrees, making the answer ![]()
See also
| 2007 AMC 12A (Problems • Answer Key • Resources) | |
| Preceded by Problem 7 |
Followed by Problem 9 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()