2009 AMC 12B Problems/Problem 24
Problem
For how many values of ![]() in
in ![]() is
is ![]() ?
Note: The functions
?
Note: The functions ![]() and
and ![]() denote inverse trigonometric functions.
denote inverse trigonometric functions.
![]()
Solution 1
First of all, we have to agree on the range of ![]() and
and ![]() . This should have been a part of the problem statement -- but as it is missing, we will assume the most common definition:
. This should have been a part of the problem statement -- but as it is missing, we will assume the most common definition: ![]() and
and ![]() .
.
Hence we get that ![]() , thus our equation simplifies to
, thus our equation simplifies to ![]() .
.
Consider the function ![]() . We are looking for roots of
. We are looking for roots of ![]() on
on ![]() .
.
By analyzing properties of ![]() and
and ![]() (or by computing the derivative of
(or by computing the derivative of ![]() ) one can discover the following properties of
) one can discover the following properties of ![]() :
:
 .
. is increasing and then decreasing on
is increasing and then decreasing on ![$[0,\pi/6]$](//latex.artofproblemsolving.com/6/c/2/6c2b88355429e009436df68cc912104a62f90dad.png) .
. is decreasing and then increasing on
is decreasing and then increasing on ![$[\pi/6,2\pi/6]$](//latex.artofproblemsolving.com/5/b/4/5b42b75565813a9ea75bd5a661689508d13d3022.png) .
. is increasing and then decreasing on
is increasing and then decreasing on ![$[2\pi/6,3\pi/6]$](//latex.artofproblemsolving.com/7/c/4/7c4b5e589270e2fed2f1e01488199a3b8ba7b165.png) .
.
For ![]() we have
we have ![]() . Hence
. Hence ![]() has exactly one root on
has exactly one root on ![]() .
.
For ![]() we have
we have ![]() . Hence
. Hence ![]() is negative on the entire interval
is negative on the entire interval ![]() .
.
Now note that ![]() . Hence for
. Hence for ![]() we have
we have ![]() , and we can easily check that
, and we can easily check that ![]() as well.
as well.
Thus the only unknown part of ![]() is the interval
is the interval ![]() . On this interval,
. On this interval, ![]() is negative in both endpoints, and we know that it is first increasing and then decreasing. Hence there can be zero, one, or two roots on this interval.
is negative in both endpoints, and we know that it is first increasing and then decreasing. Hence there can be zero, one, or two roots on this interval.
To prove that there are two roots, it is enough to find any ![]() from this interval such that
from this interval such that ![]() .
.
A good guess is its midpoint, ![]() , where the function
, where the function ![]() has its local maximum. We can evaluate:
has its local maximum. We can evaluate:
![]() .
.
Summary: The function ![]() has
has ![]() roots on
roots on ![]() : the first one is
: the first one is ![]() , the second one is in
, the second one is in ![]() , and the last two are in
, and the last two are in ![]() .
.
Actual solutions are ![]() ,
, ![]() ,
, ![]() , and
, and ![]() .
.
Solution 2
Since ![]() for all
for all ![]() , the equation reduces to
, the equation reduces to ![]() . Since
. Since ![]() for all
for all ![]() ,
, ![]() . To make the problem easier, we will measure angles in degrees. We will consider each sixth of the interval
. To make the problem easier, we will measure angles in degrees. We will consider each sixth of the interval ![]() .
.
For ![]() ,
, ![]() is in the first quadrant. Thus,
is in the first quadrant. Thus, ![]() . Setting this equal to
. Setting this equal to ![]() yields the solution
yields the solution ![]() .
.
For ![]() ,
, ![]() is in the second quadrant. Thus,
is in the second quadrant. Thus, ![]() . This yields the solution
. This yields the solution ![]() .
.
For ![]() ,
, ![]() is in the third quadrant. Thus,
is in the third quadrant. Thus, ![]() . As
. As ![]() is not on the interval
is not on the interval ![]() , this yields no solution.
, this yields no solution.
For ![]() ,
, ![]() is in the fourth quadrant. Thus,
is in the fourth quadrant. Thus, ![]() . As
. As ![]() is not on the interval
is not on the interval ![]() , this yields no solution.
, this yields no solution.
For ![]() ,
, ![]() is in the first quadrant plus a full revolution. Thus,
is in the first quadrant plus a full revolution. Thus, ![]() . This yields the solution
. This yields the solution ![]() .
.
For ![]() ,
, ![]() is in the second quadrant plus a full revolution. Thus
is in the second quadrant plus a full revolution. Thus ![]() . This yields the solution
. This yields the solution ![]() .
.
There are ![]() solutions,
solutions, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() .
.
Solution 3
Algebraically, the inverse function of a function should just cancel out, leaving ![]() . However, upon inspection we find that the graphs of these "inverse function of the function" equations are also periodic, like their normal trig function counterparts, due to the fact that inverse trig functions will never return any angle value higher than
. However, upon inspection we find that the graphs of these "inverse function of the function" equations are also periodic, like their normal trig function counterparts, due to the fact that inverse trig functions will never return any angle value higher than ![]() . But instead of a smooth wave, these graphs are made up of zigzags with slope
. But instead of a smooth wave, these graphs are made up of zigzags with slope ![]() and
and ![]() . Trying a few values, we see that
. Trying a few values, we see that
![]()
peaks at ![]() and
and
![]()
peaks at ![]()
But we want the graph of ![]() , which has a period of
, which has a period of ![]() instead of
instead of ![]() . So this means the interval
. So this means the interval ![]() will show
will show ![]() periods instead of
periods instead of ![]() of a period. Visually it would be lines with slopes
of a period. Visually it would be lines with slopes ![]() and
and ![]() . Using the graph paper given to us, we plot out the two equations according to the above and we see that they intersect
. Using the graph paper given to us, we plot out the two equations according to the above and we see that they intersect ![]() times
times ![]() .
.
Solution 4
The most conventional domain and range for ![]() is
is ![]() and
and ![]() . For
. For ![]() ,
, ![]() and
and ![]() . Since the domain of
. Since the domain of ![]() is equal to the range of
is equal to the range of ![]() , and the range of
, and the range of ![]() is equal to the domain of
is equal to the domain of ![]() ,
, ![]() .
.
Meaning that ![]() ,
, ![]() .
.
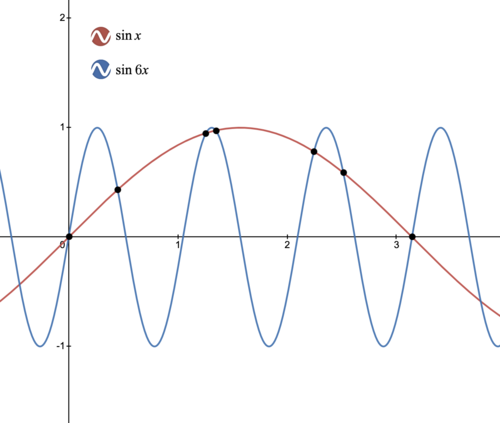
By graphing ![]() and
and ![]() together, it can be seen that there are 7 intersections for
together, it can be seen that there are 7 intersections for ![]() .
.
However, the range of ![]() is
is ![]() . Therefore
. Therefore ![]() for
for ![]() . There are
. There are ![]() solutions for
solutions for ![]() .
.
The ![]() solutions are respectively:
solutions are respectively:
![]() ,
, ![]()
![]() ,
, ![]()
![]() ,
, ![]()
![]() ,
, ![]()
See Also
| 2009 AMC 12B (Problems • Answer Key • Resources) | |
| Preceded by Problem 23 |
Followed by Problem 25 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
These problems are copyrighted © by the Mathematical Association of America, as part of the American Mathematics Competitions. ![]()