2013 AIME I Problems/Problem 13
Contents
[hide]Problem
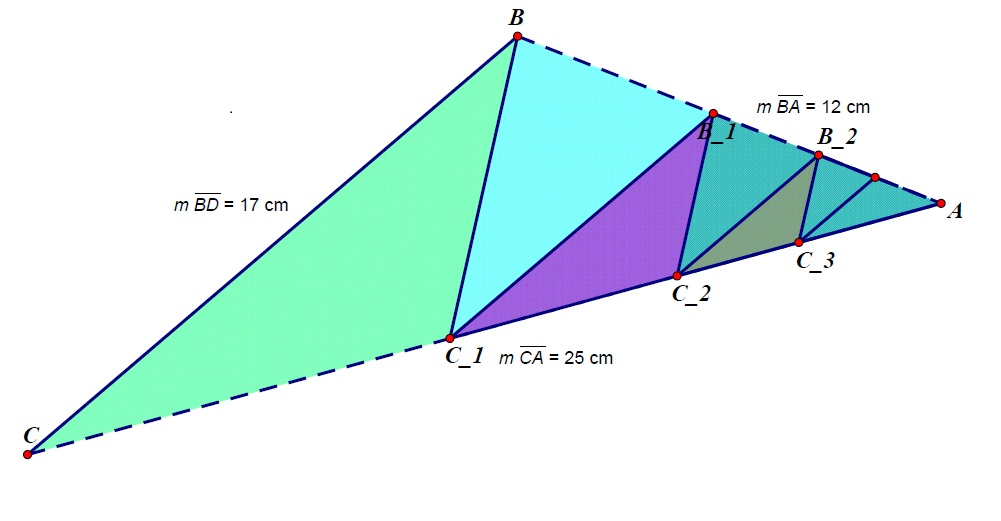
Triangle ![]() has side lengths
has side lengths ![]() ,
, ![]() , and
, and ![]() . For each positive integer
. For each positive integer ![]() , points
, points ![]() and
and ![]() are located on
are located on ![]() and
and ![]() , respectively, creating three similar triangles
, respectively, creating three similar triangles ![]() . The area of the union of all triangles
. The area of the union of all triangles ![]() for
for ![]() can be expressed as
can be expressed as ![]() , where
, where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]() .
.
Solution 1
Note that every ![]() is parallel to each other for any nonnegative
is parallel to each other for any nonnegative ![]() . Also, the area we seek is simply the ratio
. Also, the area we seek is simply the ratio ![]() , because it repeats in smaller and smaller units. Note that the area of the triangle, by Heron's formula, is 90.
, because it repeats in smaller and smaller units. Note that the area of the triangle, by Heron's formula, is 90.
For ease, all ratios I will use to solve this problem are with respect to the area of ![]() . For example, if I say some area has ratio
. For example, if I say some area has ratio ![]() , that means its area is 45.
, that means its area is 45.
Now note that ![]() 1 minus ratio of
1 minus ratio of ![]() minus ratio
minus ratio ![]() . We see by similar triangles given that ratio
. We see by similar triangles given that ratio ![]() is
is ![]() . Ratio
. Ratio ![]() is
is ![]() , after seeing that
, after seeing that ![]() , . Now it suffices to find 90 times ratio
, . Now it suffices to find 90 times ratio ![]() , which is given by 1 minus the two aforementioned ratios. Substituting these ratios to find
, which is given by 1 minus the two aforementioned ratios. Substituting these ratios to find ![]() and clearing out the
and clearing out the ![]() , we see that the answer is
, we see that the answer is ![]() , which gives
, which gives ![]() .
.
Solution 2
Using Heron's Formula we can get the area of the triangle ![]() .
.
Since ![]() then the scale factor for the dimensions of
then the scale factor for the dimensions of ![]() to
to ![]() is
is ![]()
Therefore, the area of ![]() is
is ![]() . Also, the dimensions of the other sides of the
. Also, the dimensions of the other sides of the ![]() can be
easily computed:
can be
easily computed: ![]() and
and ![]() . This allows us to compute one side of the
triangle
. This allows us to compute one side of the
triangle ![]() ,
, ![]() . Therefore, the scale factor
. Therefore, the scale factor ![]() to
to ![]() is
is ![]() , which yields the length of
, which yields the length of ![]() as
as ![]() .
Therefore, the scale factor for
.
Therefore, the scale factor for ![]() to
to ![]() is
is ![]() . Some more algebraic manipulation will show that
. Some more algebraic manipulation will show that ![]() to
to ![]() is still
is still ![]() . Also, since the triangles are disjoint, the area of the union is the sum of the areas. Therefore, the area is the geometric series
. Also, since the triangles are disjoint, the area of the union is the sum of the areas. Therefore, the area is the geometric series
![]() At this point, it may be wise to "simplify"
At this point, it may be wise to "simplify" ![]() .
So the geometric series converges to
.
So the geometric series converges to
 .
Using the difference of squares, we get
.
Using the difference of squares, we get ![]() , which simplifies to
, which simplifies to ![]() . Cancelling all common factors, we get the reduced fraction
. Cancelling all common factors, we get the reduced fraction ![]() . So
. So ![]() , yielding the answer
, yielding the answer ![]() .
.
Solution 3
For this problem, the key is to find the ![]() .
.
The area of the biggest triangle is ![]() according to the Heron's formula easily
according to the Heron's formula easily
Firstly, we discuss the ratio of ![]()
Since the problem said that two triangles are similar, so ![]() ,
,
Getting that ![]() , which is not hard to find that
, which is not hard to find that ![]() , Since
, Since ![]() ,
,
we can find the ratio of ![]() , the common ratio between two similar triangles is
, the common ratio between two similar triangles is ![]() , the similar triangles means two consecutive
, the similar triangles means two consecutive ![]()
Now the whole summation of ![]()
The desired answer is ![]() Which our answer is
Which our answer is ![]()
~bluesoul ~Marshall_Huang (some minor latex stuff}
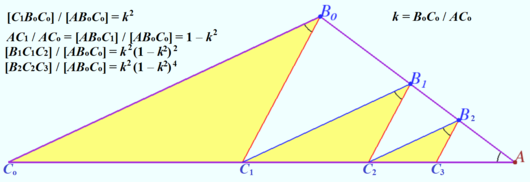
Solution 4
Let ![]() be the coefficient of the similarity of triangles
be the coefficient of the similarity of triangles
![]() Then area
Then area ![]()
The height of triangles ![]() and
and ![]() from
from ![]() is the same
is the same ![]()
The coefficient of the similarity of triangles ![]() is
is ![]()
Analogically the coefficient of the similarity of triangles ![]() is
is ![]() and so on.
and so on.
The yellow area ![]() is
is ![]()
The required area is ![]()
The number ![]() is prime,
is prime, ![]() is integer but not
is integer but not ![]() therefore the answer is
therefore the answer is ![]() .
.
vladimir.shelomovskii@gmail.com, vvsss
Video Solution
https://youtu.be/IdM24SLrxQw?si=mu5fQ-_rFZM4ud2_
~MathProblemSolvingSkills.com
Video Solution by mop 2024
~r00tsOfUnity
See also
| 2013 AIME I (Problems • Answer Key • Resources) | ||
| Preceded by Problem 12 |
Followed by Problem 14 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()