2015 AMC 10A Problems/Problem 19
Contents
[hide]Problem
The isosceles right triangle ![]() has right angle at
has right angle at ![]() and area
and area ![]() . The rays trisecting
. The rays trisecting ![]() intersect
intersect ![]() at
at ![]() and
and ![]() . What is the area of
. What is the area of ![]() ?
?
![]()
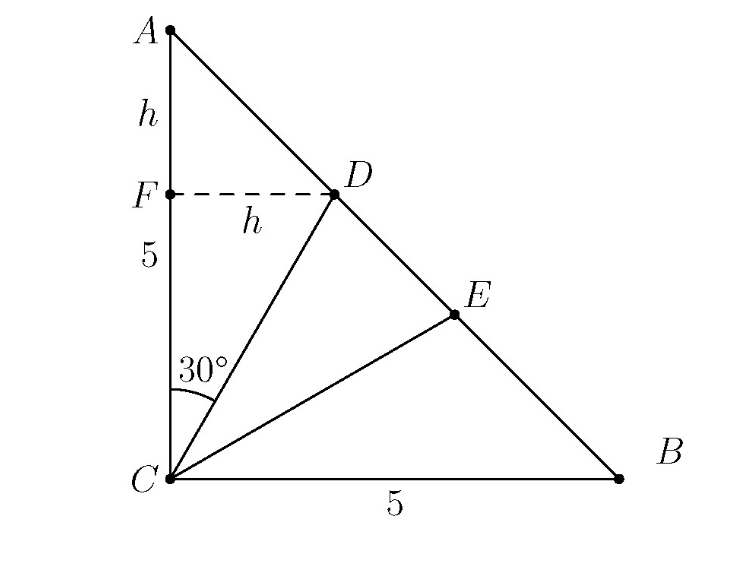
Solution 1 (No Trigonometry)
![]() can be split into a
can be split into a ![]() right triangle and a
right triangle and a ![]() right triangle by dropping a perpendicular from
right triangle by dropping a perpendicular from ![]() to side
to side ![]() . Let
. Let ![]() be where that perpendicular intersects
be where that perpendicular intersects ![]() .
.
Because the side lengths of a ![]() right triangle are in ratio
right triangle are in ratio ![]() ,
, ![]() .
.
Because the side lengths of a ![]() right triangle are in ratio
right triangle are in ratio ![]() and
and ![]() ,
, ![]() .
.
Setting the two equations for ![]() equal to each other,
equal to each other, ![]() .
.
Solving gives ![]() .
.
The area of ![]() .
.
![]() is congruent to
is congruent to ![]() , so their areas are equal.
, so their areas are equal.
A triangle's area can be written as the sum of the figures that make it up, so ![]() .
.
![]() .
.
Solving gives ![]() , so the answer is
, so the answer is 
Note
Another way to get ![]() is that you assume
is that you assume ![]() to be equal to
to be equal to ![]() , as previously mentioned, and
, as previously mentioned, and ![]() is equal to
is equal to ![]() .
. ![]()
Solution 2 (Trigonometry)
The area of ![]() is
is ![]() , and so the leg length of
, and so the leg length of ![]()
![]() is
is ![]() Thus, the altitude to hypotenuse
Thus, the altitude to hypotenuse ![]() ,
, ![]() , has length
, has length ![]() by
by ![]() right triangles. Now, it is clear that
right triangles. Now, it is clear that ![]() , and so by the Exterior Angle Theorem,
, and so by the Exterior Angle Theorem, ![]() is an isosceles
is an isosceles ![]() triangle. Thus,
triangle. Thus, ![]() by the Half-Angle formula, and so the area of
by the Half-Angle formula, and so the area of ![]() is
is ![]() . The answer is thus
. The answer is thus 
Solution 3 (Analytical Geometry)
Because the area of triangle ![]() is
is ![]() , and the triangle is right and isosceles, we can quickly see that the leg length of the triangle
, and the triangle is right and isosceles, we can quickly see that the leg length of the triangle ![]() is 5. If we put the triangle on the coordinate plane, with vertex
is 5. If we put the triangle on the coordinate plane, with vertex ![]() at the origin, and the hypotenuse in the first quadrant, we can use slope-intercept form and tangents to get three lines that intersect at the origin,
at the origin, and the hypotenuse in the first quadrant, we can use slope-intercept form and tangents to get three lines that intersect at the origin, ![]() , and
, and ![]() . Then, you can use the distance formula to get the length of
. Then, you can use the distance formula to get the length of ![]() . The height is just
. The height is just ![]() , so the area is just
, so the area is just 
Solution 4 (Weak Trigonometry)
Just like with Solution 1, we drop a perpendicular from ![]() onto
onto ![]() , splitting it into a
, splitting it into a ![]() -
-![]() -
-![]() triangle and a
triangle and a ![]() -
-![]() -
-![]() triangle. We find that
triangle. We find that ![]() .
.
Now, since ![]() by ASA,
by ASA, ![]() . Since,
. Since, ![]() ,
, ![]() . By the sine area formula,
. By the sine area formula, ![]()
Solution 5 (Basic Trigonometry)
Prerequisite knowledge for this solution: the side ratios of a 30-60-90, and 45-45-90 right triangle.
We let point C be the origin. Since ![]() and
and ![]() trisect
trisect ![]() , this means
, this means ![]() and the equation of
and the equation of ![]() is
is ![]() (you can figure out that the tangent of 30 degrees gives
(you can figure out that the tangent of 30 degrees gives ![]() ). Next, we can find A to be at
). Next, we can find A to be at ![]() and B at
and B at ![]() , so the equation of
, so the equation of ![]() is
is ![]() . So we have the system:
. So we have the system:
![\[\begin{cases}y=\frac{\sqrt{3}}{3}x\\y=-x+5\end{cases}\]](http://latex.artofproblemsolving.com/5/5/7/557ee710ae7a14c71ea2506fac7ddd96b5e6bf84.png)
By substituting values, we can arrive at ![]() , or
, or ![]() . We multiply
. We multiply ![]() .
.
Dropping an altitude from E onto ![]() , and calling the intersection point G, we find that
, and calling the intersection point G, we find that ![]() is a 45-45-90 triangle with a leg of
is a 45-45-90 triangle with a leg of ![]() . Thus,
. Thus, ![]() .
.
Dropping an altitude from C onto ![]() , and calling the intersection point H, we find that
, and calling the intersection point H, we find that ![]() , and by the theorem of betweenness applied to H, E, and B, we get
, and by the theorem of betweenness applied to H, E, and B, we get ![]() .
.
We are almost done. By symmetry, ![]() , so to find the area of the triangle CED, we only need to multiply HE by CH,
, so to find the area of the triangle CED, we only need to multiply HE by CH, ![]() . This is answer choice
. This is answer choice  ~JH. L
~JH. L
Solution 6 (Law of Sines)
We know that the area of the right triangle is ![]() and that the two legs are equal, so we can easily tell that the length of the two legs is
and that the two legs are equal, so we can easily tell that the length of the two legs is ![]() . Thus, the hypotenuse
. Thus, the hypotenuse ![]() and
and ![]() Let's quickly define
Let's quickly define ![]() as the point that bisects
as the point that bisects ![]() and
and ![]() . Then, we can say that the area of the desired triangle is
. Then, we can say that the area of the desired triangle is ![]() .
Let
.
Let ![]() Since
Since ![]() is one of the trisecting points of
is one of the trisecting points of ![]() Because
Because
![]()
![]() Now, we can employ the Law of Sines. It tells us that
Now, we can employ the Law of Sines. It tells us that ![]() . Plugging in our angle values, we get that
. Plugging in our angle values, we get that ![]() It's easy to find that
It's easy to find that ![]() and that
and that ![]() . Plugging in these values into our previous equation, we get
. Plugging in these values into our previous equation, we get ![]() Cross multiplying gets us
Cross multiplying gets us ![]() and then we simplify like so:
and then we simplify like so: ![]()
![]()
![]() Now, using our definition of
Now, using our definition of ![]() , we know that
, we know that ![]() =
= ![]() . We want to put this under one common denominator, which is pretty simple to execute. That leaves us with
. We want to put this under one common denominator, which is pretty simple to execute. That leaves us with ![]()
![]()
![]()
![]()
![]() Whew. That was longer than expected. Anyways, quick inspection tells us that
Whew. That was longer than expected. Anyways, quick inspection tells us that ![]() so now we just have to do some simplifying to find the desired,
so now we just have to do some simplifying to find the desired, ![]() . Let's do that now.
. Let's do that now.
![]()
![]()
![]() (We need to take a quick conjugation break. Note that
(We need to take a quick conjugation break. Note that ![]() )
)
![]()
![]()
![\[[CDE] =\boxed{\frac{50 - 25\sqrt{3}}{2} \text{(D)}.}\]](http://latex.artofproblemsolving.com/f/e/f/fef82dbd932c857cceed58a39e8e47e8f8569579.png) ~Nickelslordm
~Nickelslordm
Solution 7(Ratio of 15,75,90 triangle)
Drawing the two rays, we get triangles CAD, CDE, and CBE. Notice that triangles CAD and CBE are identical, and triangle CDE is an isosceles triangle with angles CDE=CED=75 and angle DEC=15.
We draw the height of triangle ABC, which is also the height of triangle CDE. Because triangle CDE is an isosceles triangle, we know the height spilt base DE into 2 equal parts, and triangle CDE into 2 identical 15,75,90 triangle. From the ratio of 15,75,90 triangles,we know that the ratio of the height and half of line DE is equal to the ratio of areas.
Video Solution:
https://www.youtube.com/watch?v=JWMIsCS0Ksk
https://www.youtube.com/watch?v=_LPz_i4Cwv4
See Also
| 2015 AMC 10A (Problems • Answer Key • Resources) | ||
| Preceded by Problem 18 |
Followed by Problem 20 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()